How do you use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by y =x^3, y= 8 , x= 0 revolved about the x-axis?
1 Answer
Volume
Explanation:
If you imagine an almost infinitesimally thin vertical line of thickness
delta A ~~"width" xx "height" = ydeltax = f(x)deltax
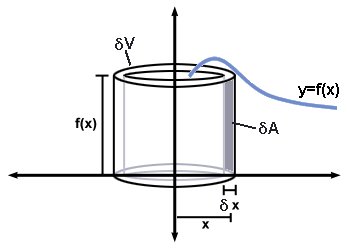
If we then rotated this infinitesimally thin vertical line about
delta V~~ 2pi xx "radius" xx "thickness" = 2pixdeltaA=2pixf(x)deltax
If we add up all these infinitesimally thin cylinders then we would get the precise total volume
V=int_(x=a)^(x=b)2pi \ x \ f(x) \ dx
Similarly if we rotate about
V=int_(y=a)^(y=b)2pi \ y \ g(y) \ dy
So for this problem we have:
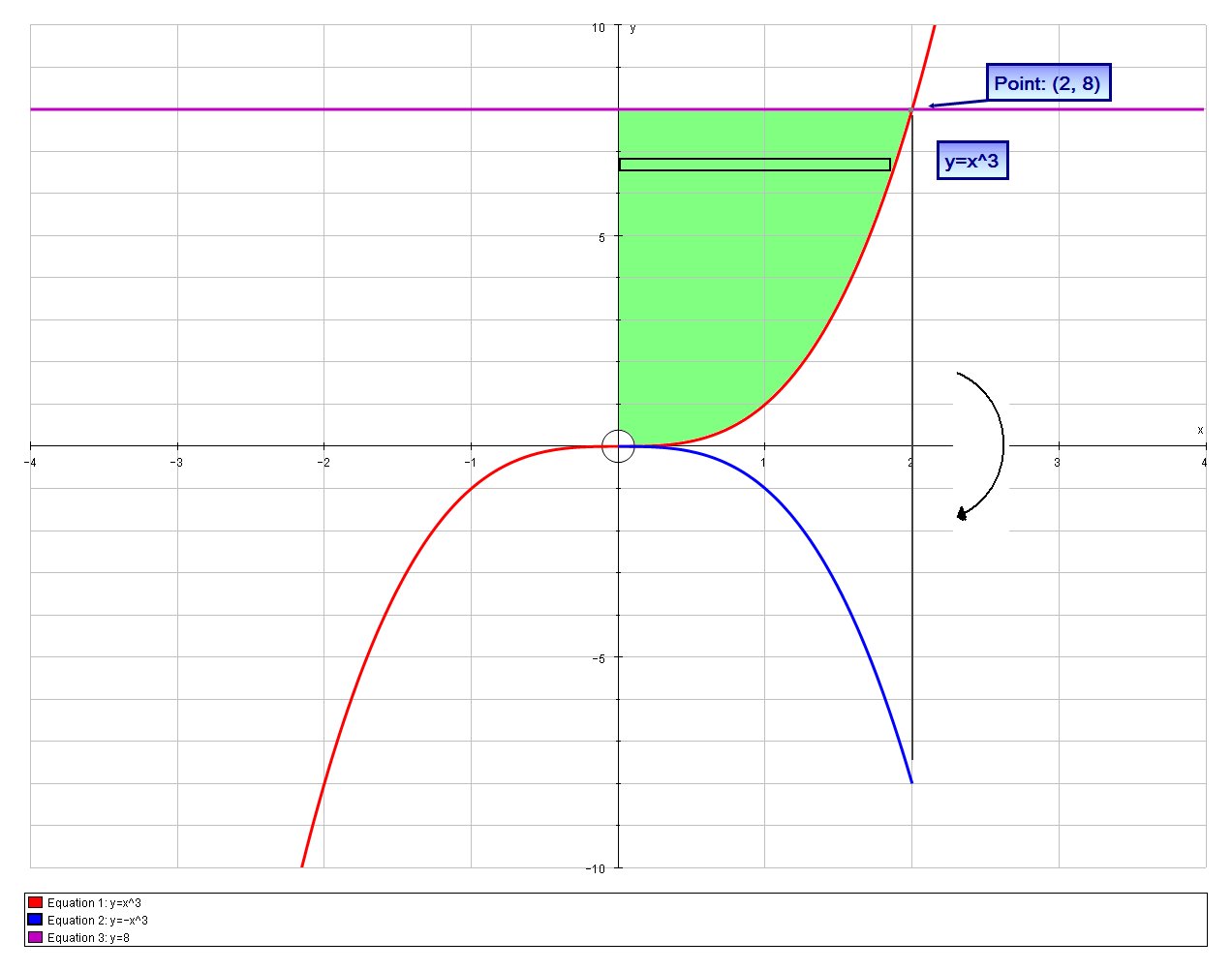
We need the point of intersection for the bounds of integration;
x \ = 0 => y=0
x^3 = 8=>x=2
And we are integrating wrt
y=x^3 => x=y^(1/3)
Then the required volume is given by:
V=int_(y=a)^(y=b)2pi \ y \ g(y) \ dy
\ \ \= 2pi int_0^8 \ y*y^(1/3) \ dy
\ \ \= 2pi int_0^8 \ y^(4/3) \ dy
\ \ \= 2pi [y^(7/3)/(7/3)]_0^8
\ \ \= (6pi)/7 [y^(7/3)]_0^8
\ \ \= (6pi)/7 (8^(7/3)-0)
\ \ \= (6pi)/7 * 128
\ \ \= (768pi)/7 \ \ \ unit^3
Washer Method
We call also use the "washer" method which gives the volume of revolution about
V=pi \ int_(x=a)^(x=b) \ (f(x))^2 \ dx
Which in this problem gives:
V="(volume bounded by " y=8) - ("volume bounded by " y=x^3)
Volume bounded by
V=pi \ int_0^2 \ (x^3)^2 \ dx
\ \ \ =pi \ int_0^2 \ x^6 \ dx
\ \ \ =pi \ [x^7/7]_0^2
\ \ \ =pi \ (128/7 - 0)
\ \ \ =(128pi)/7
The required volume of revolution is then the volume of a cylinder (
V=(pi)(64)(2) - (128pi)/7
\ \ \ =128pi - (128pi)/7
\ \ \ =(768pi)/7 , as before
Or if you prefer, we can perform the calculation in a single integral, as:
V="(volume bounded by " y=8) - ("volume bounded by " y=x^3)
\ \ \ =pi \ int_0^2 \ (8)^2 \ dx - pi \ int_0^2 \ (x^3)^2 \ dx
\ \ \ =pi \ int_0^2 \ (8)^2 - (x^3)^2 \ dx
\ \ \ =pi \ int_0^2 \ 64-x^6 dx
\ \ \ =pi \ [64x-x^7/7]_0^2
\ \ \ =pi \ (128-128/7 - 0)
\ \ \ =(768pi)/7 , as before

