Question

How do you use the quadratic formula to solve `12sin^2x-13sinx+3=0` in the interval `[0,2pi)`?

Answer 1

The solutions are `S={0.34,0.848,2.294,2.802}rd`

Explanation:

Our equation is

`12sin^2x-13sinx+3=0`

The quadratic equation is

`ax^2+bx+c=0`

We start by calculating the discriminant

`Delta=b^2-4ac=(-13)^2-4*(12)*(3)`

`=169-144=25`

As,

`Delta>0`, there are 2 real solutions

So,

The solutions are

`x=(-b+-sqrtDelta)/(2a)`

`sinx=((13)+-5)/24`

`sinx=18/24=3/4` or `sinx=8/24=1/3`

The values of `x` are

`x=arcsin(3/4)` and `arcsin(1/3)`

`x=0.848rd`, `x=2.294rd`, `x=0.34rd` and `x=2.802rd`

Answer 2

`x~~0.3398`, `x~~0.8481`, `x=2.294`, and `x=2.802` radians.

Explanation:

Strategy: Rewrite this equation as a quadratic equation using `u=sin(x)`. Solve the quadratic equation for `u` by factoring. Then replace `u` with `sin(x)` again and solve using `arcsin`.

Step 1. Rewrite this equation as a quadratic using `color(red)u=color(red)sin(x)`

You are given
`12(color(red)(sin(x)))^2-13(color(red)(sin(x)))+3=0`

Replace `color(red)(sin(x))` with `color(red)(u)`
`12color(red)(u)^2-13color(red)(u)+3=0`

Step 2. Factor the quadratic equation.
`(3u-1)(4u-3)=0`

Solving gives us
`3u-1=0` and `4u-3=0`
`u=1/3` and `u=3/4`

Step 3. Replace `u` with `sin(x)` again and solve with `arcsin`
`sin(x)=1/3` and `sin(x)=3/4`

`sin^(-1)(sin(x))=sin^(-1)(1/3)` and `sin^(-1)(sin(x))=sin^(-1)(3/4)`

`x~~0.3398` radians and `x~~0.8481` radians

These answer work because we were asked to find the solutions in `[0,2pi]~~[0,6.2832]`

However, the graph of `y=12(sin(x))^2-13(sin(x))+3` is

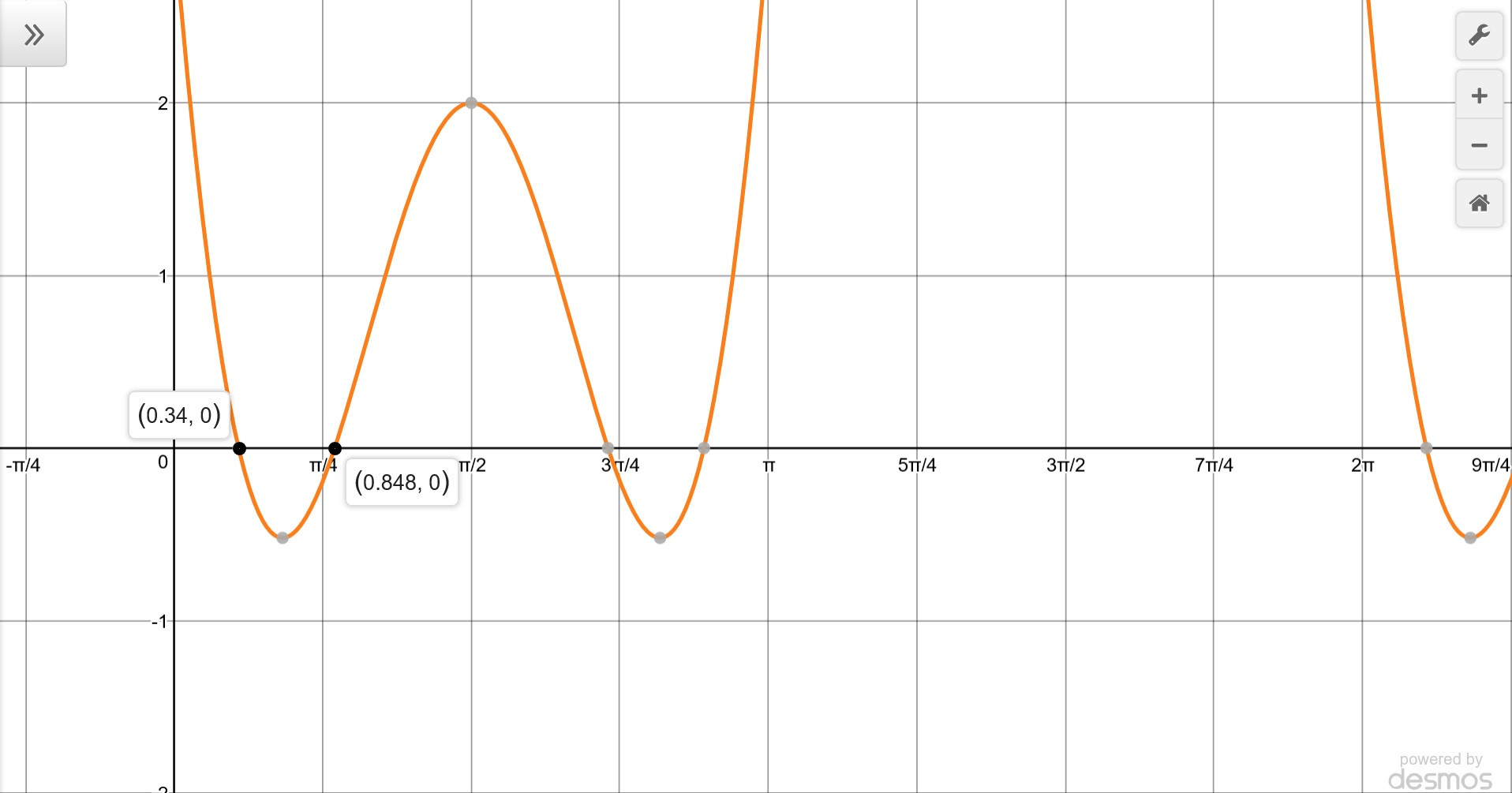
Which shows four solutions in the interval `[0,2pi]`, not two.

We must find the other solutions by recognizing that sine functions are periodic with respect to `pi`

So, `x=pi-0.8481=2.294` and `x=pi-0.3398=2.802`

The other two solutions are
`x=2.294` and `x=2.802`