Question

How do you use the rational roots theorem to find all possible zeros of `f(x) = 6x^4 + 4x^3 - 2x^2 + 2`?

Answer 1

There are no Real zeros for the given equation.

Explanation:

If we attempt to use the Rational Root Theorem by testing
`color(white)("XXX")x=+-abs("factors of " 2)/abs("factors of " 6)`
in `f(x)=6x^44x^3-2x^2+2`
the candidate values would be:
`color(white)("XXX")+-{1,1/2,1/3,1/6,cancel(1/2),cancel(2/2),2/3,cancel(2/6)}`
but as indicated in the table below, none of these give a zero result:

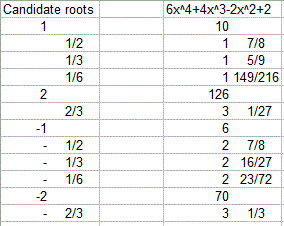
Therefore there are no rational zeros for this expression.

In fact, if we consider the graph for this expression, we can see that it has no Real zeros.
graph{6x^4+4x^3-2x+2 [-8.036, 9.754, -0.84, 8.05]}

`6x^4+4x^3-2x^2+2` should have `4` imaginary zeroes, but they can not be determined using the Rational Factor Theorem.