How do you use the rational roots theorem to find all possible zeros of #f(x)=x^5-3x^2-4#?
1 Answer
Find
We can find numerical approximations:
#x_1 ~~ 1.6477#
#x_(2,3) ~~ 0.151952+-1.03723i#
#x_(4,5) ~~ -0.975801+-1.12111i#
Explanation:
#f(x) = x^5-3x^2-4#
By the rational roots theorem, any rational zeros of
That means that the only possible rational zeros are:
#+-1, +-2, +-4#
None of these work, so
In common with most quitics and polynomials of higher degree, the zeros of this one cannot be expressed in terms of
It is possible to find numerical approximations for the zeros using a method like Durand-Kerner.
For example, we can use this C++ program...
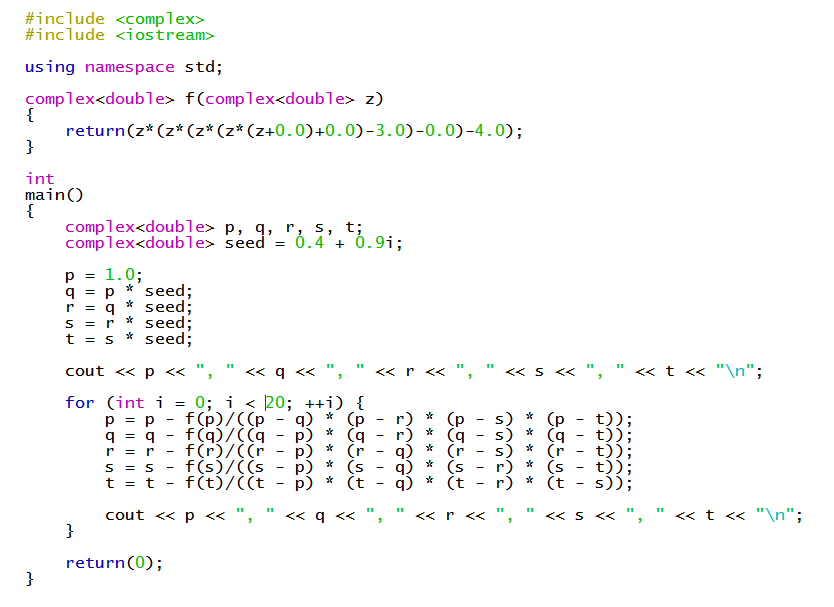
to find numerical approximations for the zeros:
#x_1 ~~ 1.6477#
#x_(2,3) ~~ 0.151952+-1.03723i#
#x_(4,5) ~~ -0.975801+-1.12111i#
For a little more explanation of the method see https://socratic.org/s/ax2iiWhR

