How do you use the second derivative test to find min/max/pt of inflection of #y= x^5-5x#?
1 Answer
Jul 6, 2015
Maximum at
Minimum at
Inflection point at
Explanation:
Start by taking the first derivative:
set it equal to zero:
Now we find the second derivative:
we analyze the sign of the second derivative by setting it bigger than zero:
so this is true when
we have an inflection point at
Graphically:
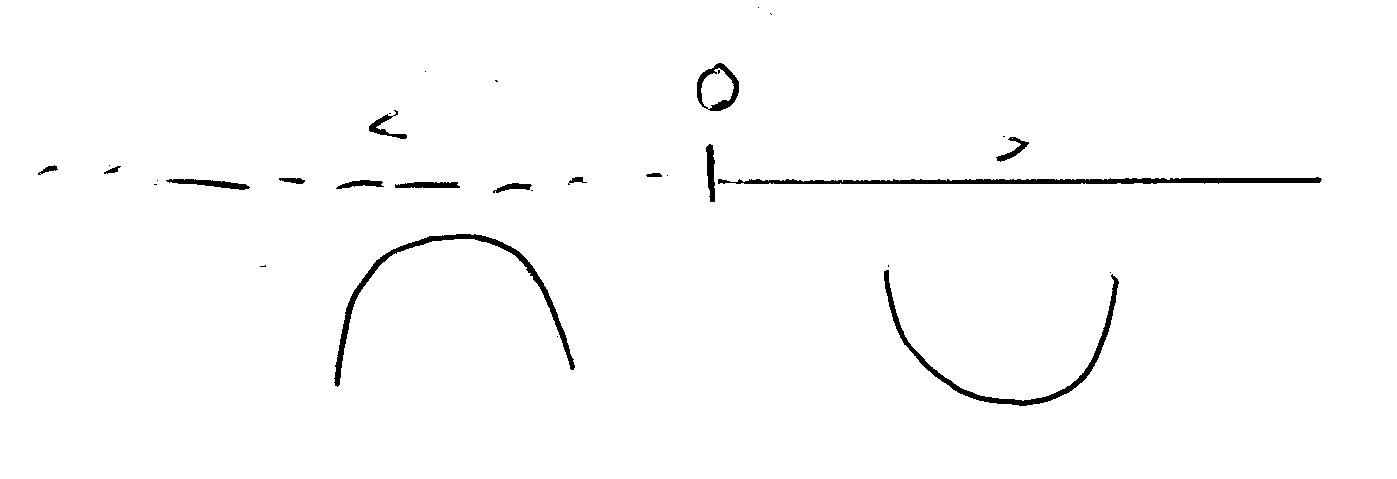
With this we discover that :
The graph of your fnction looks like:
graph{x^5-5x [-10, 10, -5, 5]}

