How do you use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region y=x+2 and y=x^2 rotated about the x axis?
1 Answer
See the explanation section, below.
Explanation:
Graph the region, including the points of intersection,
In order to use shells, we must take our representative slices parallel to the axis of rotation. So the thickness of each shell will be
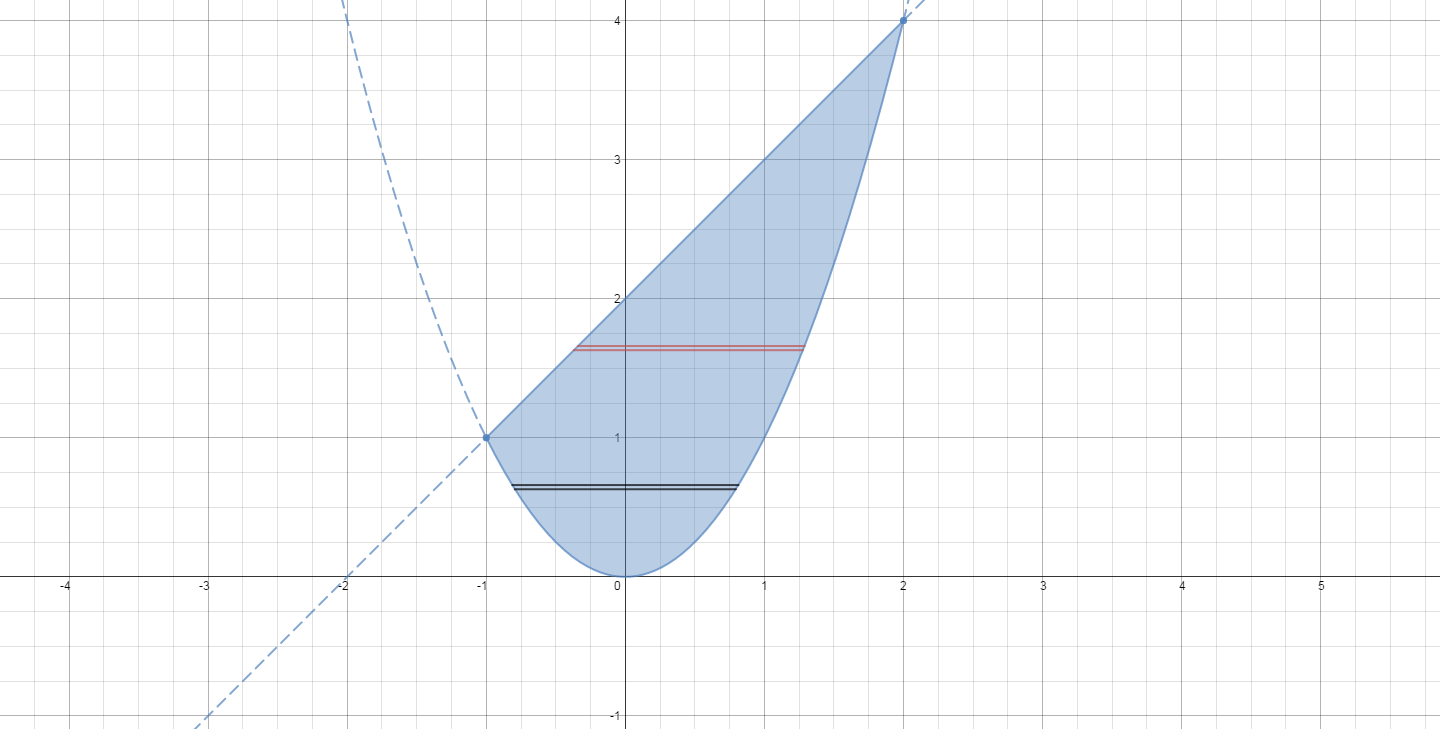
The thickness of each shell will be
And the limits of integration are
The volume of the representative shell is
The radius of each shell will be
The "height" of each cylindrical shell will be the distance between the
Notice in the picture, that as
From
So we need
From
So we need
The total volume is

