If we have been through the proof of #lim_(thetararr0)sintheta/theta = 1#, then we have seen that for small, positive #theta#, we have:
#0 < sintheta < theta#.
(Or perhaps it was pointed out in our study of trigonometry. See note, below.)
So, for large positive #x#, we have
#0 < sin(1/x) < 1/x#.
Observe that #sqrtx> 0#, so we can multiply without reversing the inequalities.
#0 < sqrtx sin(1/x) < 1/sqrtx#
#lim_(xrarroo)0 = 0 = lim_(xrarroo)1/sqrtx#.
Therefore,
#lim_(xrarroo)sqrtxsin(1/x) = 0#.
Note
Here is a picture reminder for #0 < theta < pi/2# that #0 < sintheta < theta#. (This is not a rigorous proof, simply a reminder.)
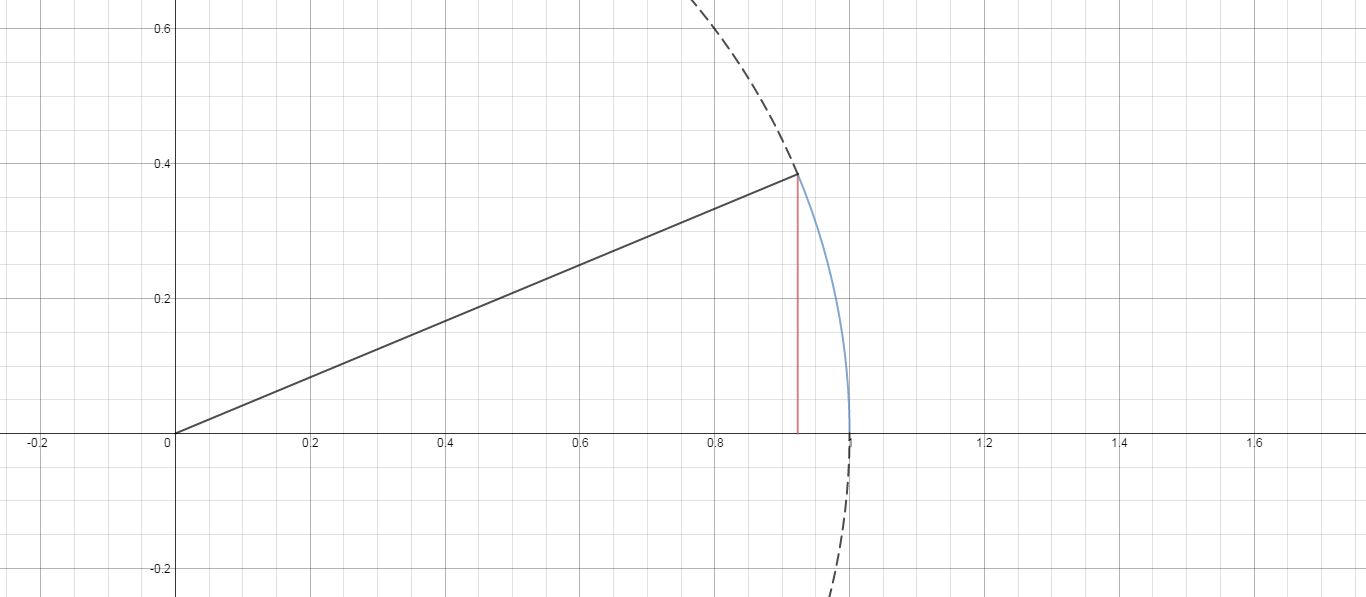
For the angle measuring #theta# radians, note the point on the unit circle associated with #theta#.
#sintheta# is the vertical distance from the point to the #x#-axis (red line segent),
while #theta# is the length of the arc from the point to the #x# axis (blue arc).
Because the perpendicular distance is the shortest, we believe that, for small positive #theta#,
#0 < sintheta < theta#


