Question

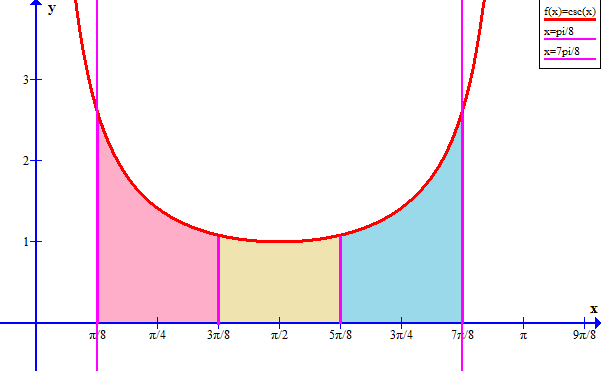
How do you use the Trapezoidal rule and three subintervals to give an estimate for the area between `y=cscx` and the x-axis from `x= pi/8` to `x = 7pi/8`?

Answer 1

Approximately `3.75` square units

Explanation:

Dividing the given interval `[pi/8,(7pi)/8]`
into 3 equal width intervals (each with a width of `pi/4`:
`color(white)("XXX")I_1=[pi/8,(3pi)/8]`
`color(white)("XXX")I_2=[(3pi)/8,(5pi)/8]`
`color(white)("XXX")i_3=[(5pi)/8,(7pi)/8]`

[from this point on, extensive use of spreadsheet/calculator is recommended]

Evaluating `csc(x)` at each interval edge:
`color(white)("XXX")csc(pi/8)=2.6131259298`
`color(white)("XXX")csc((3pi)/8)=1.0823922003`
`color(white)("XXX")csc((5pi)/8)=1.0823922003`
`color(white)("XXX")csc((7pi)/8)=2.6131259298`

The area of each interval trapezoid is calculated as
`color(white)("XXX")`the average of the 2 edge lengths times the strip width.

`"Area"_(I1)=(2.6131259298+1.0823922003)/2 xx pi/4`
`color(white)("XXXX")=1.4512265761`

Similarly we can calculate
`"Area"_(I2)=0.8501088462`

`"Area"_(I3)=1.4512265761`

and the Sum of these Areas gives an approximation of the integral value:
`int_(pi/8)^((7pi)/8)csc(x) dx~~3.7525619983`

Answer 2

`int_(pi/8)^((7pi)/8) \ cscx \ dx ~~ 3.7526 \ \ (4dp)`

Explanation:

We have:

`y = cscx`

We want to estimate `int \ y \ dx` over the interval `[pi/8,(7pi)/8]` with `3` strips; thus:

`Deltax = ((7pi)/8-pi/8)/3 = pi/4`

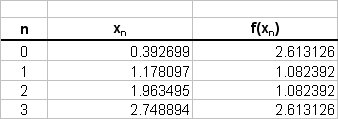
The values of the function, working to 6dp, are tabulated using Excel as follows;

Trapezium Rule

`A = int_(pi/8)^((7pi)/8) \ cscx \ dx`
`\ \ \ ~~ 0.785398/2 * { 2.613126 + 2.613126 + 2*(1.082392 + 1.082392) }`
`\ \ \ = 0.392699 * { 5.226252 + 2*(2.164784) }`
`\ \ \ = 0.392699 * { 5.226252 + 4.329569 }`
`\ \ \ = 0.392699 * 9.555821`
`\ \ \ = 3.752562`

Actual Value

For comparison of accuracy:

`A= int_(pi/8)^((7pi)/8) \ cscx \ dx`
`\ \ \ = [ color(white)(""/"") -log(abs(csc(x)+cot(x))) \ ]_(pi/8)^((7pi)/8`
`\ \ \ = 3.229781832346191`