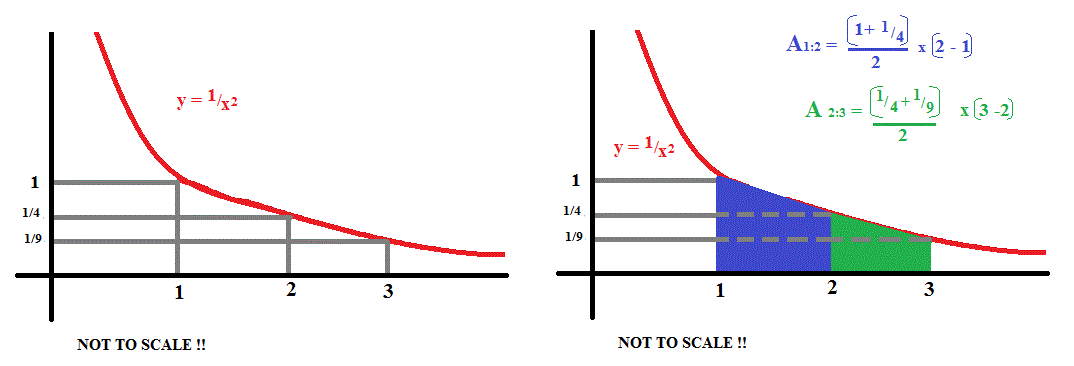
How do you use the trapezoidal rule with n=2 to approximate the area under the curve #y=1/x^2# from 1 to 3?
1 Answer
Jul 15, 2015
Draw 2 trapezoids under the curve, the first between
Explanation:
With
The first will have a width of
and an average height of
The second will also have a width of
and will have an average height of
The total area of the two trapezoids (approximating the area under the curve) is