How do you use the trapezoidal rule with n=4 to approximate the area between the curve #lnx# from 1 to 3?
1 Answer
Jan 9, 2017
# int_(1)^(3) \ ln x \ dx ~~ 1.28 " " (2dp) #
Explanation:
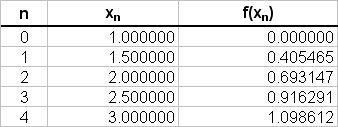
The values of
Using the trapezoidal rule:
# int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}#
We have:
# int_(1)^(3) \ ln x \ dx ~~ 0.5/2 { (0 + 1.098612) + 2(0.405465 + 0.693147 + 0.91629) } #
# 0.25 { + 1.098612 + 2(2.014903) } #
# 0.25 { + 1.098612 + 4.029806 } #
# 0.25 { + 5.128418 } #
# 1.282104 #
It is sometimes interesting to compare against the actual exact answer. Using
# int_(1)^(3) \ ln x \ dx = [xlnx - x]_(1)^(3) #
# " " = (3ln3-3) - (1ln1-1) #
# " " = (3ln3-3) - (-1) #
# " " = 3ln3-2 #
# " " = 1.295836... #