How do you use transformation to graph the cosine function and determine the amplitude and period of #y=-4cos(-3x)#?
1 Answer
May 29, 2017
As cosine is an even function we have that
so,
Hence,
If we start with the graph of
i.e. the period changes from 360 degrees to 120 degrees
From
The amplitude is 4.
See the graph below: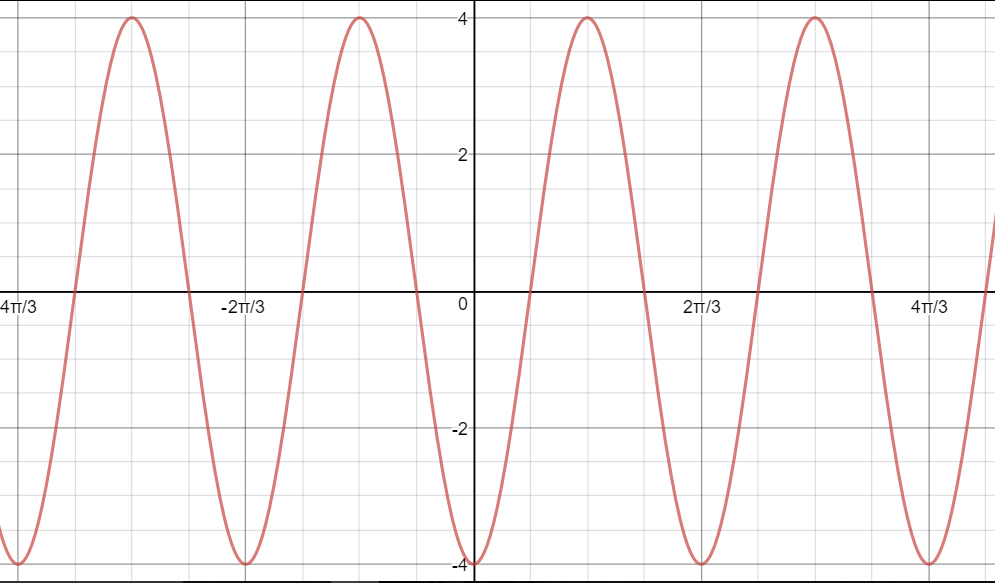
:)>

