Question

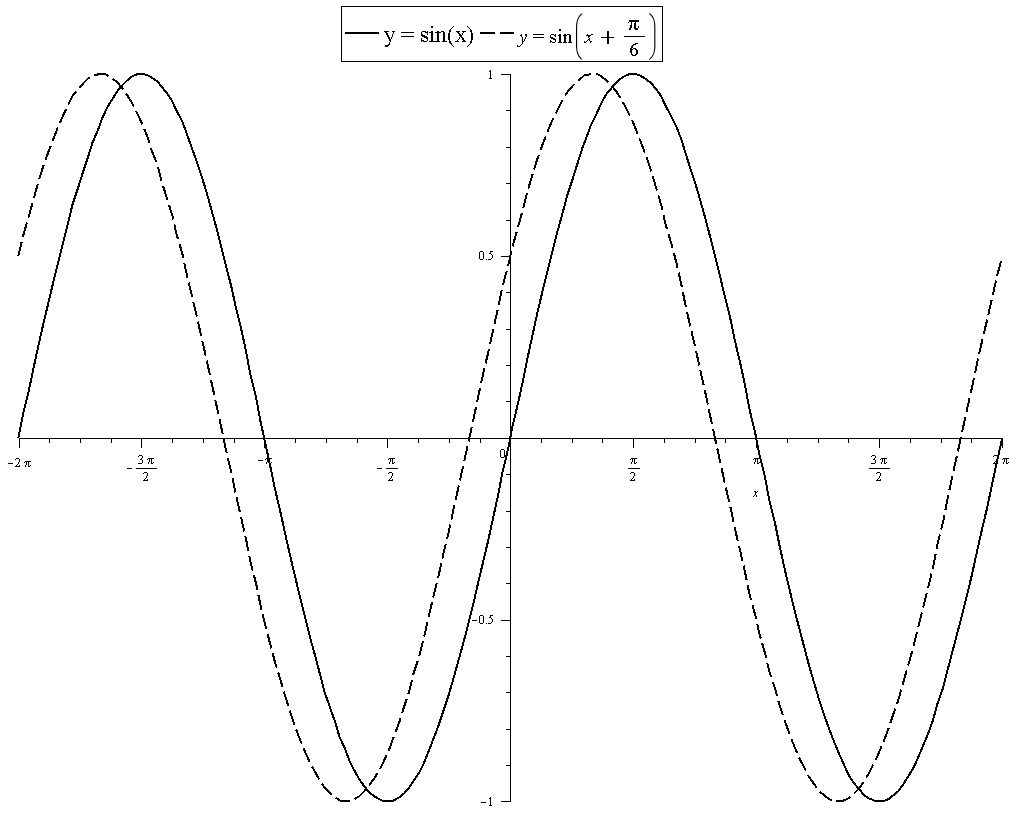
How do you use transformation to graph the sin function and determine the amplitude and period of `y=sin(x+pi/6)`?

Answer 1

See below.

Explanation:

If we look at a trig function in the form:

`y =asin(bx+c)+d`

Amplitude is `color(white)(888) color(blue)(a)`

Period is `color(white)(888)color(blue)((2pi)/b)`

Phase shift is `color(white)(888) color(blue)((-c)/b)`

Vertical shift is `color(white)(888)color(blue)(d)`

From: `y=sin(x+pi/6)`

We can see amplitude is 1. This is the same as for `y=sin(x)`

The period is: `(2pi)/1=2pi`. This is the same as `y=sinx`

Phase shift is: `(-pi/6)/1=-pi/6` This translates the graph of

`y=sinx` `color(white)(88) pi/6` units to the left.

From the above, we conclude that the graph of `y=sin(x+pi/6)` is the graph of `y=sinx` translated `pi/6` units to the left.

Graph of `y=sin(x+pi/6)` and `y=sinx` on the same axes: