How do you verify the identity #(csc x - sin x)(sec x - cos x)(tan x + cot x) = 0#?
2 Answers
Apr 23, 2015
I am not sure that is equal to zero....I got
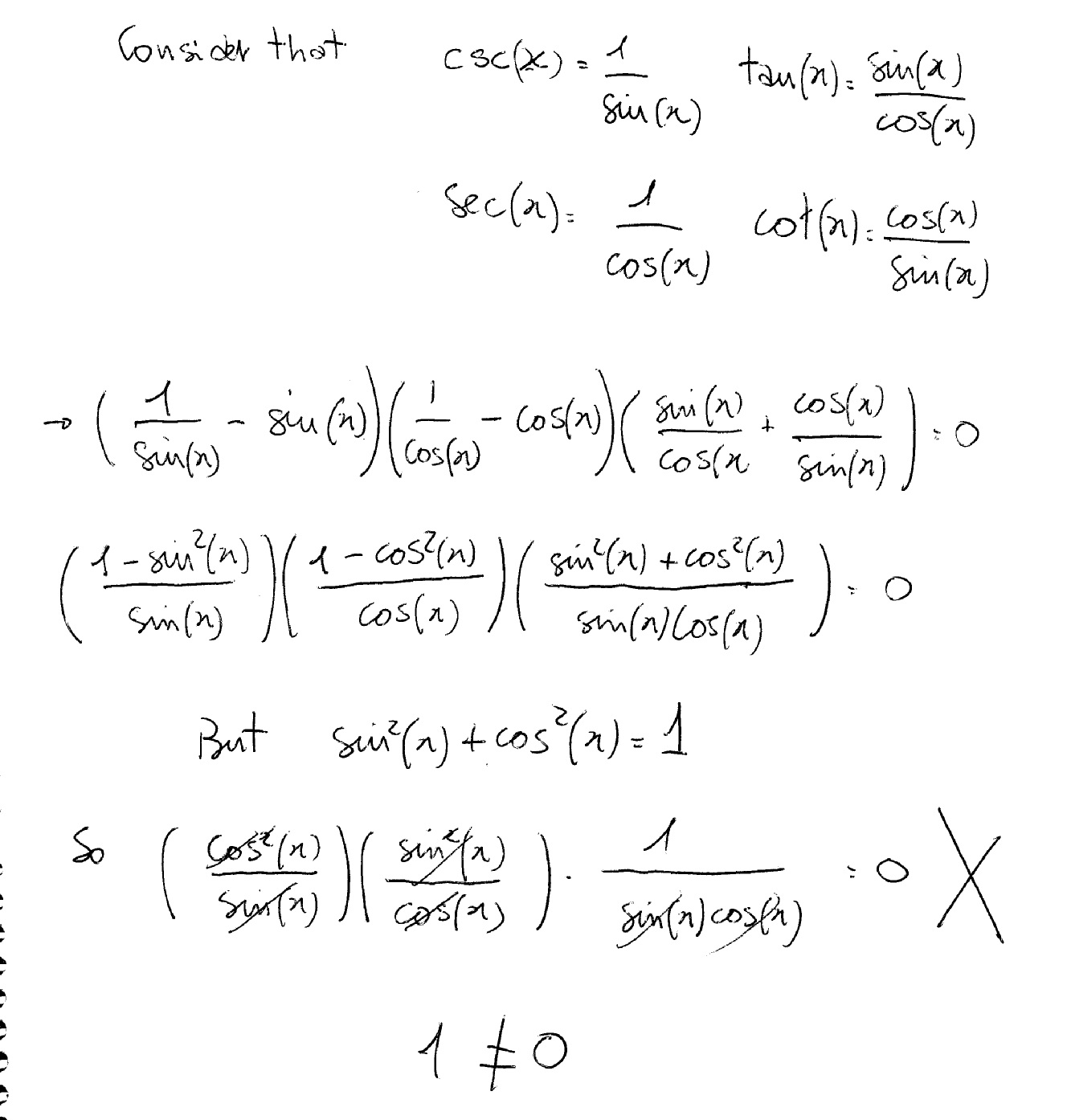
Have a look.
Apr 23, 2015
WARNING: This may not be the simplest way!
Let
and
becomes
Replacing
we get

