Question

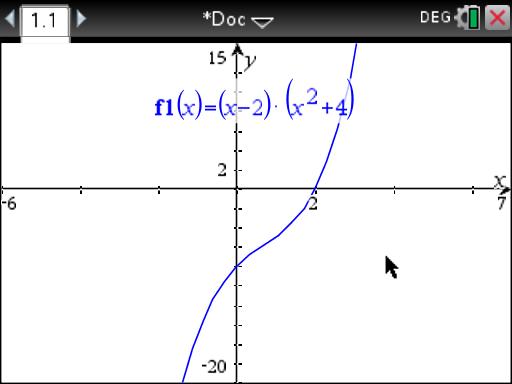
How do you write a polynomial function with the given zeros 2 and 2i and degree 3?

Answer 1

You need to write three factors: `(x - 2)( x - 2i) (x + 2i)` based on the Factor Theorem and Complex Conjugates Theorem.

Explanation:

Now, expand the expression: `(x-2)(x^2+4) = x^3-2x^2-4x-8`
Notice that the polynomial is of degree 3, called a "cubic".

Observe that the graph of the function only has one "zero" at 2. That is because the other two algebraic zeros are imaginary numbers, 2i and -2i, which can not be plotted on the real number coordinate plane: