How do you write an equation for a circle whose diameter has endpoints of (-2, 4) and (4, 12)?

Question

14231 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-08-14T22:27:48

The eqn . of circle :
#x^2+y^2-2x-16y+40=0#

Let , #A(-2,4) and B(4,12)# be the endpoints of diameter #bar(AB)# and #C# be the center of given circle.

Let #r # be the radius of circle.

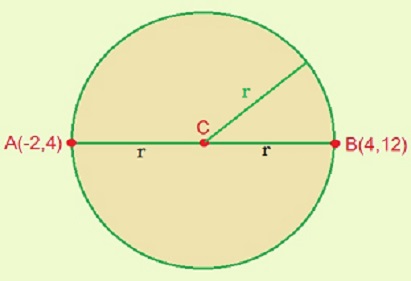
enter image source here

Here ,

Center #C# is the midpoint of diameter #bar(AB)#

So ,

#C((-2+4)/2,(4+12)/2)-=(1,8)#

Now ,,

#"Radius r="CA=CB#

#:.r=CB=sqrt((4-1)^2+(12-8)^2)=sqrt(9+16)=5#

We know that,

#"The eqn. of circle with center C(h,k) and radius r "# is

#(x-h)^2+(y-k)^2=r^2#

#:.(x-1)^2+(y-8)^2=5^2#

#:.x^2-2x+1+y^2-16y+64=25#

#:.x^2+y^2-2x-16y+40=0#

Answer 2 · 2018-08-14T22:43:03

The eqn. of circle is :
#:.x^2+y^2-2x-16y+40=0#

We know that ,

#"If "A(x_1,y_1) and B(x_2,y_2)"are the endpoints of the "#

#"diameter of the circle then the eqn. of circle is :"#

#(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0#

We have diameter #bar(AB)# ,with #A(-2,4) and B(4,12).#

So, the eqn. of circle is :

#(x-(-2))(x-4)+(y-4)(y-12)=0#

#(x+2)(x-4)+(y-4)(y-12)=0#

#:.x^2-4x+2x-8+y^2-12y-4y+48=0#

#:.x^2+y^2-2x-16y+40=0#