How do you write an equation in slope-intercept form for a line with (4, -1) and perpendicular to a line with equation 3x + y = 4?
1 Answer
Explanation:
A linear equation in the form
The given line
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If two lines are perpendicular the slope of one is the negative reciprocal of the other.
Any line perpendicular to
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
A line with a slope of
can be written in slope-point form as:
A line perpendicular to
can be written as:
which would typically be simplified as
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Here is a graph with these two equations and the required point for verification:
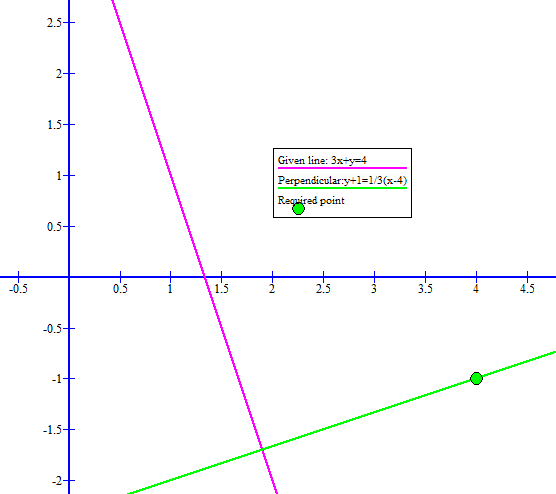
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Note 1
If you are not familiar with slope of
it can be easily derived by converting to slope intercept form:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Note 2
For some the more common general slope-point form might be
I prefer the form that I have used above since it avoids the exclusion problem when
