Question

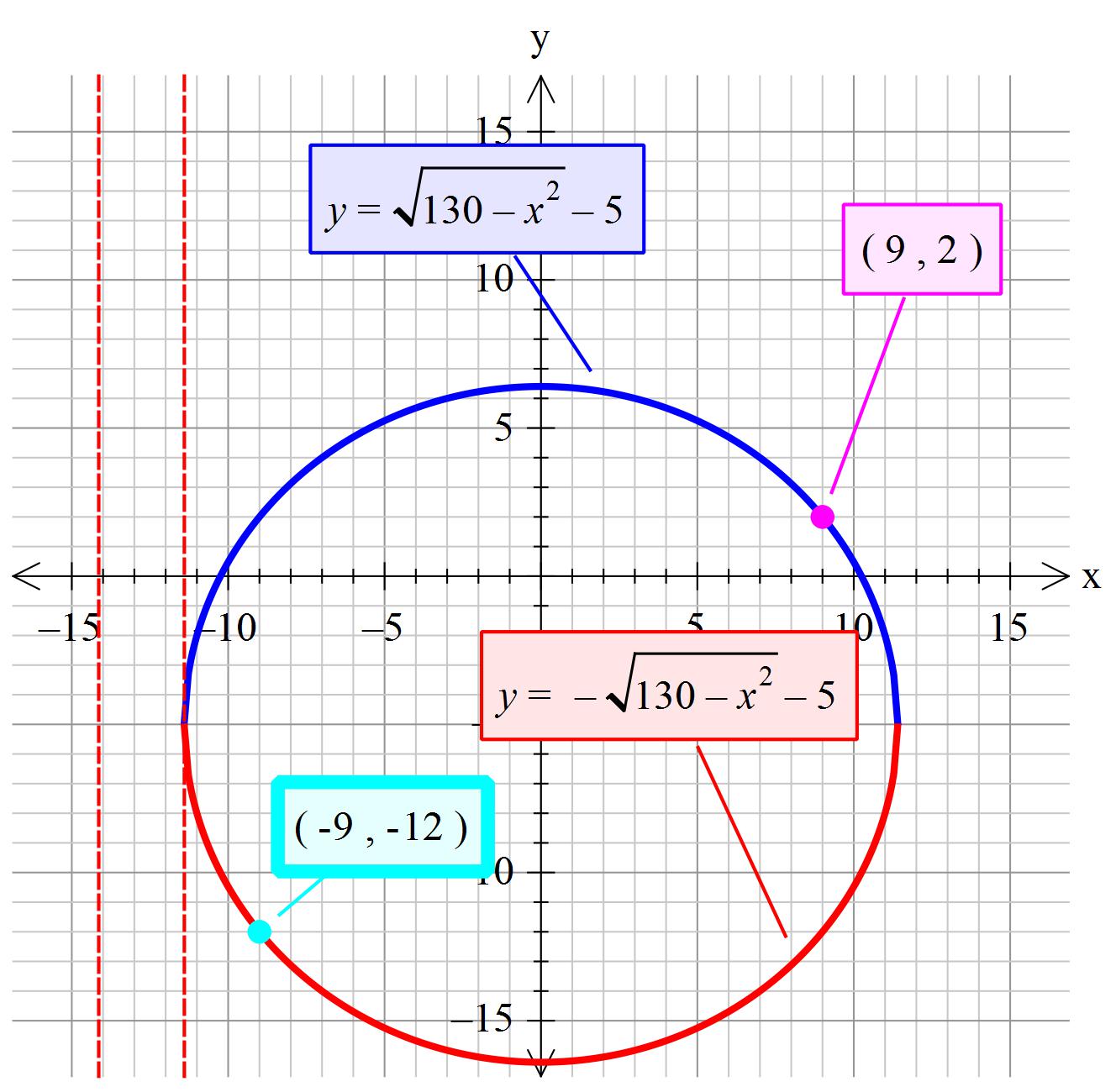
How do you write an equation in standard form of the circle with the given properties: endpoints of a diameter are (9,2) and (-9,-12)?

Answer 1

`=>(y+5)^2+x^2=r^2`

Explanation:

`color(blue)("I automatically did this bit but decided it is not needed.")` `color(blue)("However, I left it in as a demonstration of method")`

The diameter length will be the distance between (9,2) and (-9,-12)

`=>2r=sqrt( (x_2-x_1)^2+(y_2-y_1)^2)`

`=>2r=sqrt((-9-9)^2+(-12-2)^2) = sqrt(520)`

`=>2r=2sqrt(130)" "=>" "r=sqrt(130)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("This is the relevant calculation")`

Known: The equation of a circle where the centre is coincidental to the origin is `y^2+x^2=r^2`

But the centre of the circle does not coincide with the origin.
So the equation needs to be adjusted. We have to make allowance for offsetting both the x and y.

Centre of the circle is at the mean x and the mean y

Centre`->(x,y)->((9-9)/2,(2-12)/2) = (0,-5)`

So we need to 'translate' (mathematically move) the coordinates of the circles centre back to the origin to relate it to `r^2.`

`=>(y+5)^2+(x+0)^2=r^2`

`=>(y+5)^2+x^2=r^2`

`color(red)("~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~")`

Consider `(y+5)^2+x^2=r^2`

`=>y=+- sqrt (r^2-x^2)color(white)(..) -5`

Please ignore the red dotted lines. My package is doing something odd!