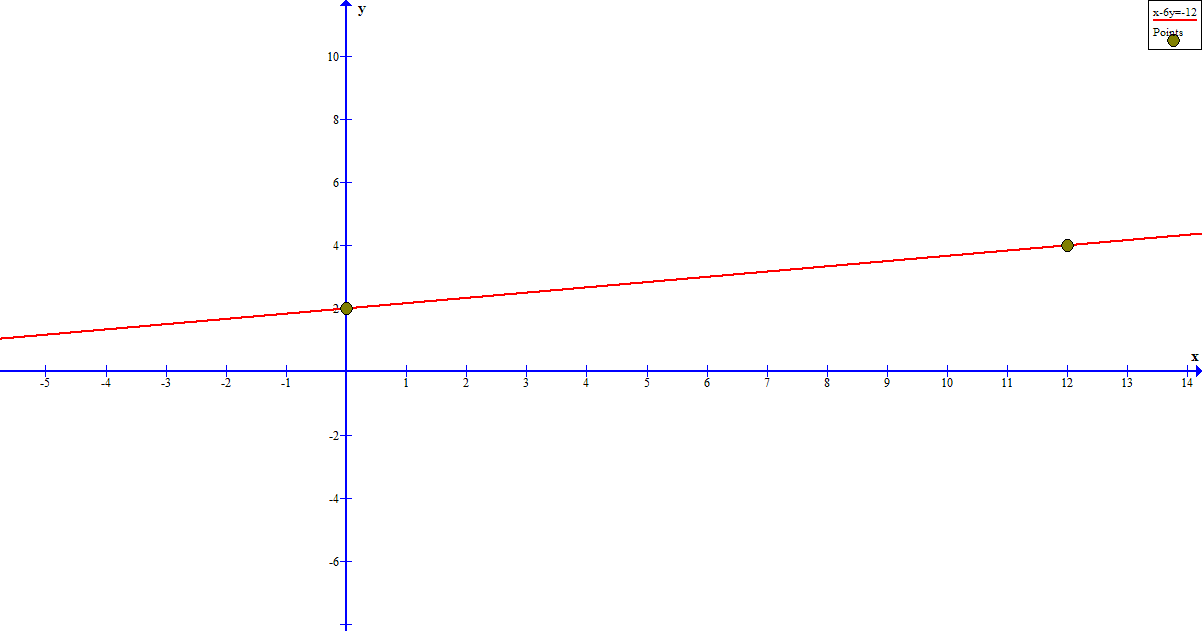
How do you write an equation of a line that has a intercept of 2 and passes through (12, 4)?
1 Answer
Oct 25, 2016
Explanation:
If the line has a y-intercept of
and since we are told that it also passes through
we can write the line's equation in two-point form as:
Simplifying:
or in standard form: