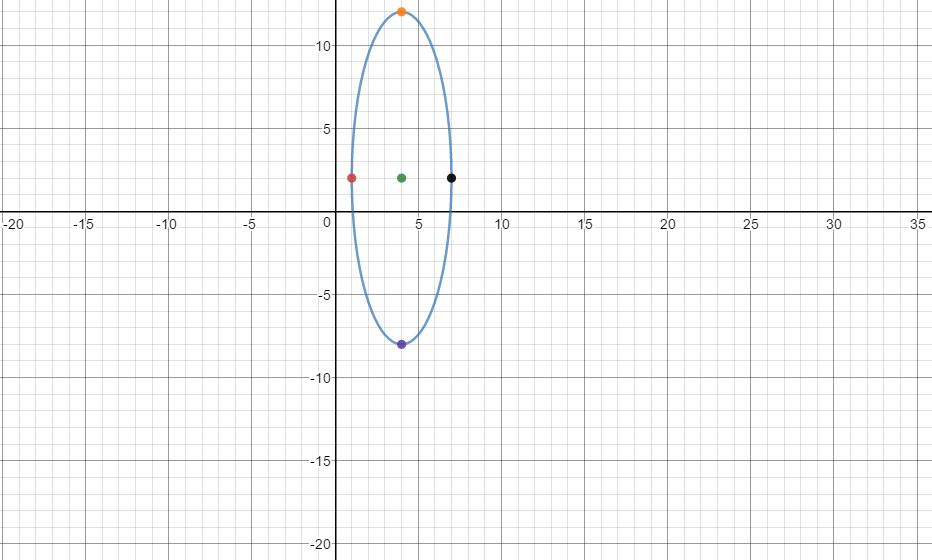
How do you write an equation of an ellipse given the major axis is 20 units long and parallel to the y-axis and the minor axis is 6 units long, center at (4,2)?
1 Answer
Jan 27, 2017
The Cartesian form of the equation of an ellipse with a vertical major axis is
where
Explanation:
Given that the center is
Given that the major axis is 20 units, substitute 10 for "a" into equation [2]:
Given that the minor axis is 6 units, substitute 3 for "b" into equation [3]:
Equation [4] is specified equation. The following graphs is ellipse with the center and the end points of the major and minor axes plotted.