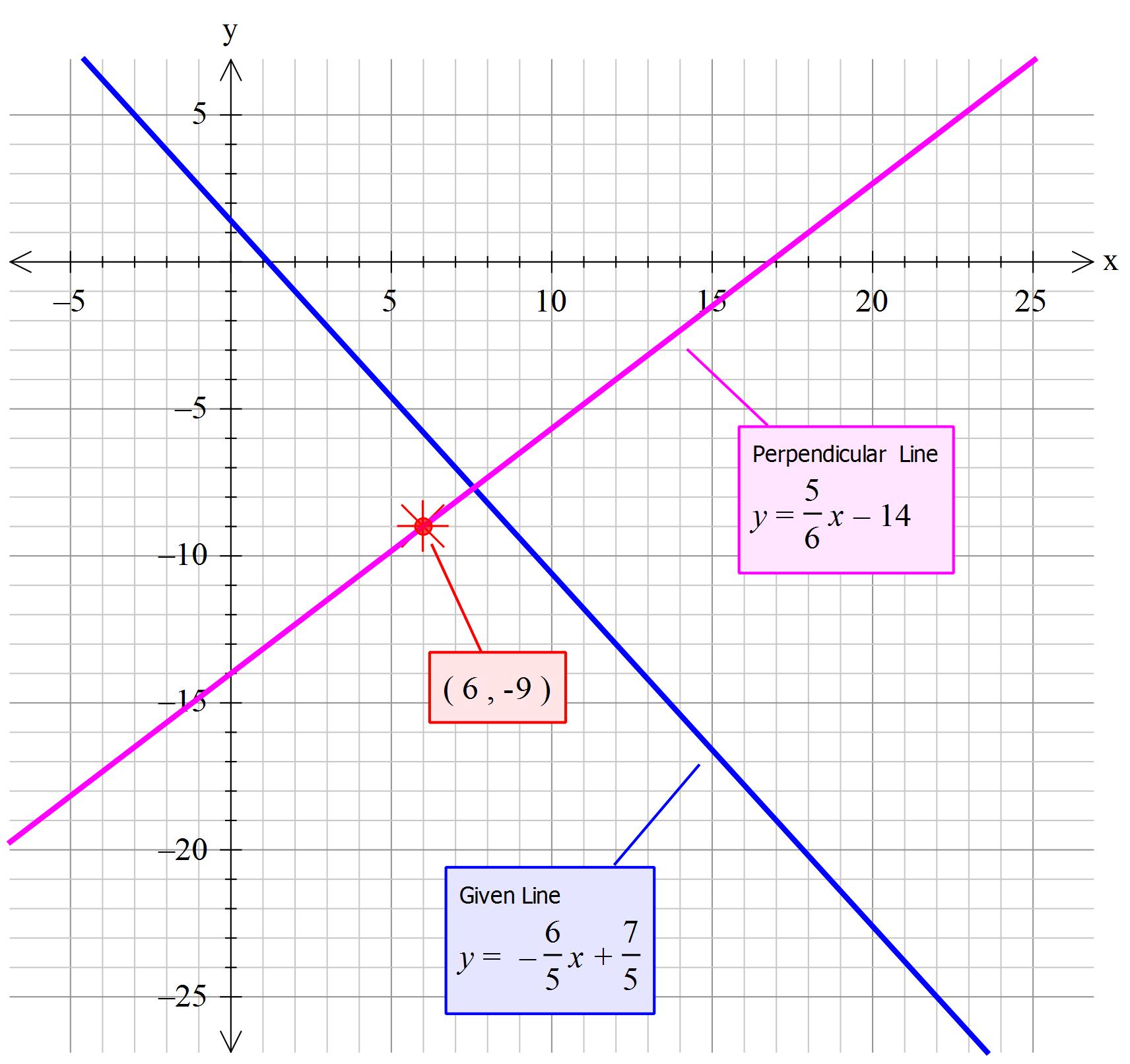
How do you write an equation of the line containing the given point and perpendicular to the given line: (6, -9); 6x+5y=7?
1 Answer
Jul 7, 2016
Explanation:
Given:
Change the equation into the standard form of
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
From this the gradient of the given line is:
So the gradient of a line perpendicular (normal) to this is:
,................................................................................................
But the second line passes through
'

