Question

How do you write an equation of the line tangent to `x^2+y^2-6x-8y=0` at the point (0,0)?

Answer 1

`y = -3/4x`

Explanation:

We have:

`x^2 + y^2 -6x - 8y = 0`

We can put this into standard form by equating `x` and `y` terms separately and completing the square on `x` and `y`

`x^2 -6x + y^2 - 8y = 0`
`(x-3)^2 - 3^2 + (y-4)^2 - 4^2 = 0`
`(x-3)^2 - 9 + (y-4)^2 - 16 = 0`
`(x-3)^2 + (y-4)^2 = 25`
`(x-3)^2 + (y-4)^2 = 5^2`

So the equation is a circle of centre `(3,4)` and radius `5`

We can verify by inspection that `(0,0)` lies on the circle

The Normal passes through the origin `(0,0)` and the centre `(3,4)`, so the Normal has gradient:

`m_N =(Delta y) / (Delta x) = (4-0)/(3-0) = 4/3`

The tangent is perpendicular to the Normal so the product of their gradients is `-1`:

`:. m_T = -1/m_N = -3/4`

So the tangent passes through the origin `(0,0)` and has gradient `m_T = -3/4` so using the straight line formula `y-y_1=m(x-x_1)` then the tangent equation is;

`y-0 = -3/4(x-0)`
`:. y = -3/4x`

We can confirm this graphically;

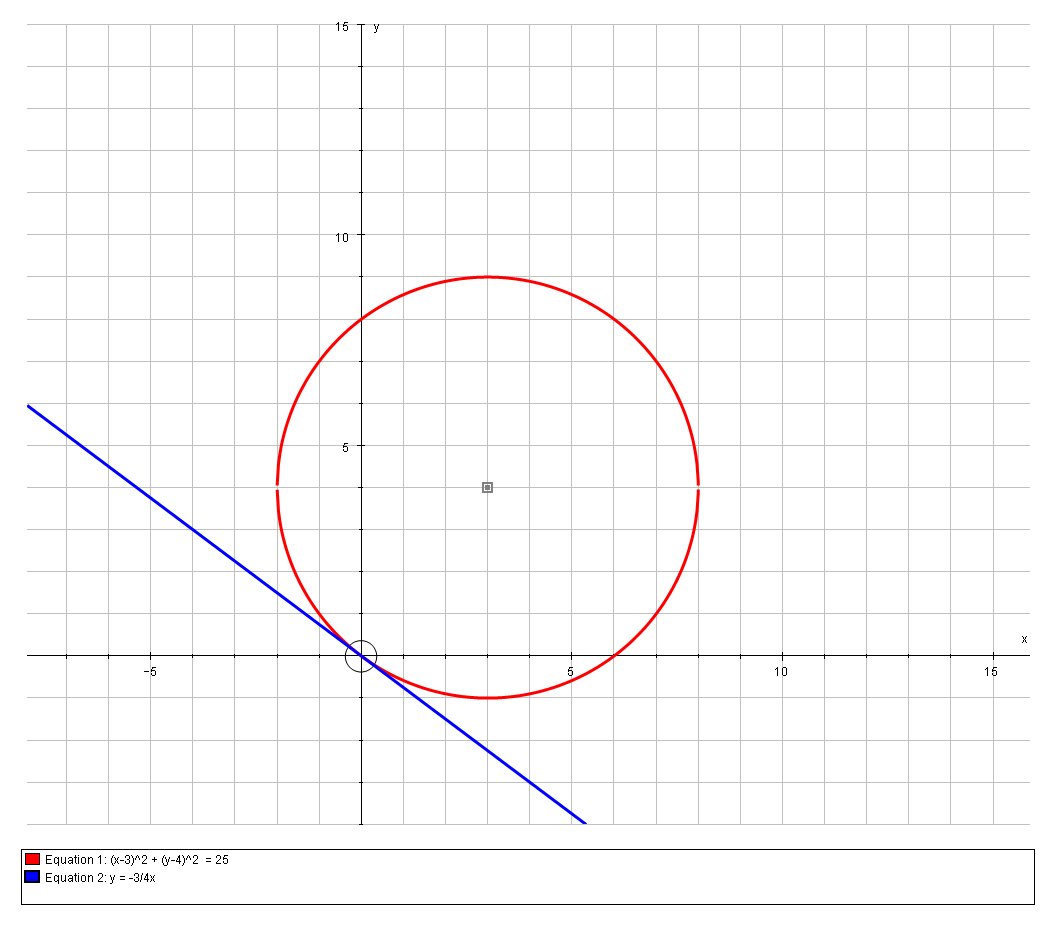
We could also use calculus by differentiating implicitly:

`x^2 + y^2 -6x - 8y = 0`
`=> 2x+2ydy/dx - 6 -8dy/dx = 0`

At `(0,0)` we have;

`0+0 - 6 -8dy/dx = 0 => dy/dx = -6/8 = -3/4`, as before