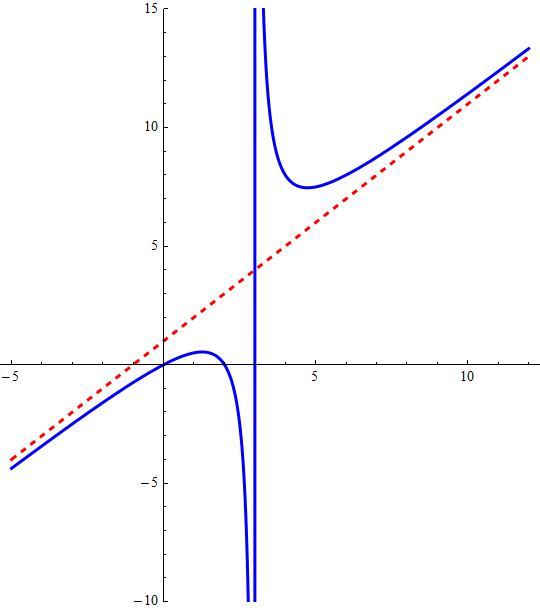
How do you write an equation with a vertical asymptote of #3#, slant asymptote of #y=x+1#, and #x# intercept at #2#?
1 Answer
Jun 22, 2016
Explanation:
Let
It has a vertical asymptote at
It has a slant symptote given by
Now, the general polynomial of degree
We know also that
then
so
Finally