How do you write #root3(x^-6)# with fractional exponent?
2 Answers
Explanation:
Note that
#roota(x^b)=x^(a//b)#
Thus,
#root3(x^-6)=x^(-6//3)=x^-2#
Note that
#x^-2=1/x^2#
both of which are acceptable answers.
Very slight expansion on the process
Explanation:
Given:
Consider the
Put it back into the root giving
This is the same as
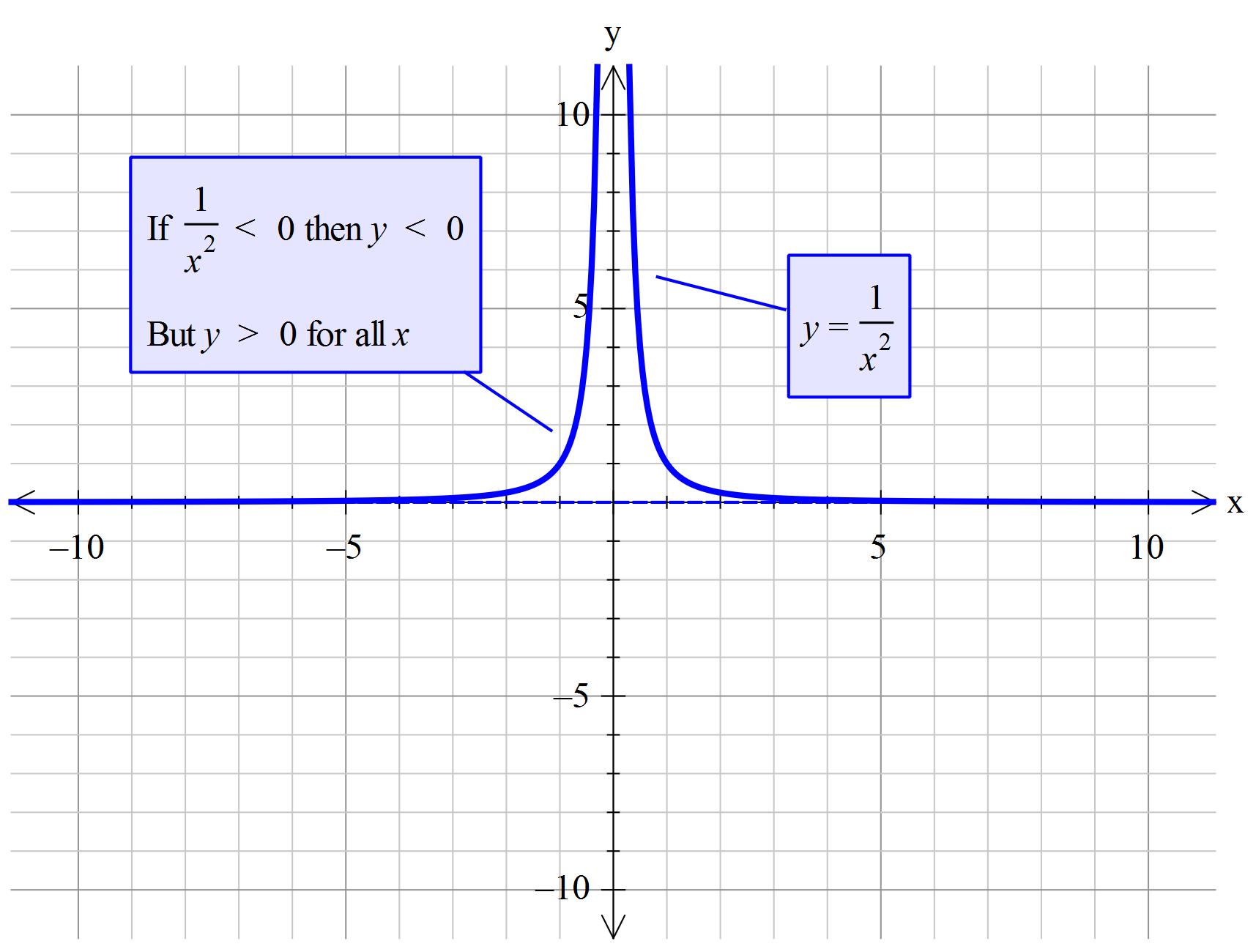
But
The key question is about the state being positive or negative.
Consider
Consider the
However the given expression has been simplified such that it involves
So it is correct to write the answer as positive. That is, we do not have negative