Question

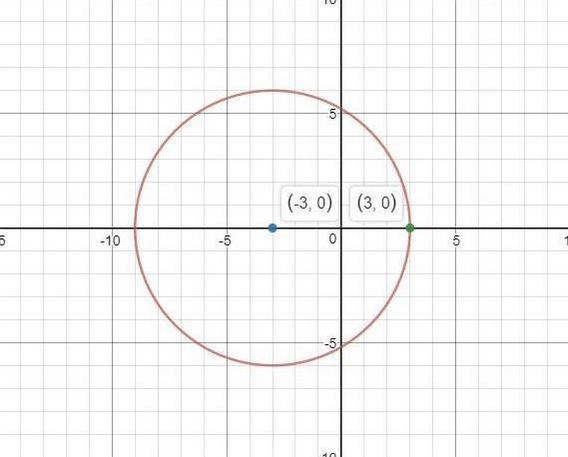
How do you write the equation for a circle with center of circle (-3,0) radius with endpoint (3,0)?

Answer 1

`(x+3)^2 + y^2 = 36`

Explanation:

The equation of a circle is `(x-h)^2 + (y-k)^2 = r^2`, where `(h,k)` is the center and `r` is the radius.

If the center is at `(-3,0)` and the endpoint of the radius is at `(3,0)`, then the length of the radius is the distance between the two points, which is `3-(-3) = 6`.

We can substitute `color(blue)((color(blue)(-3, 0))` for `(h,k)`, and `color(red)6` for `r`.

`(x-h)^2 + (y-k)^2 = r^2`

`(x- color(blue)((-3)))^2 + (y-color(blue)0)^2 = color(red)6^2`

`(x+3)^2 + y^2 = 36`

We can check this by graphing. The center of the circle is at `(-3,0)` and the endpoint of the radius is at `(3,0)`, so our equation is correct.