How do you write the equation of a circle given center (3,-7) and tangent to the y-axis?
3 Answers
Explanation:
The equation for a circle is
Plugging in
Since you want the circle to be tangent to the
A radius of 3, since the
Here's the graph:
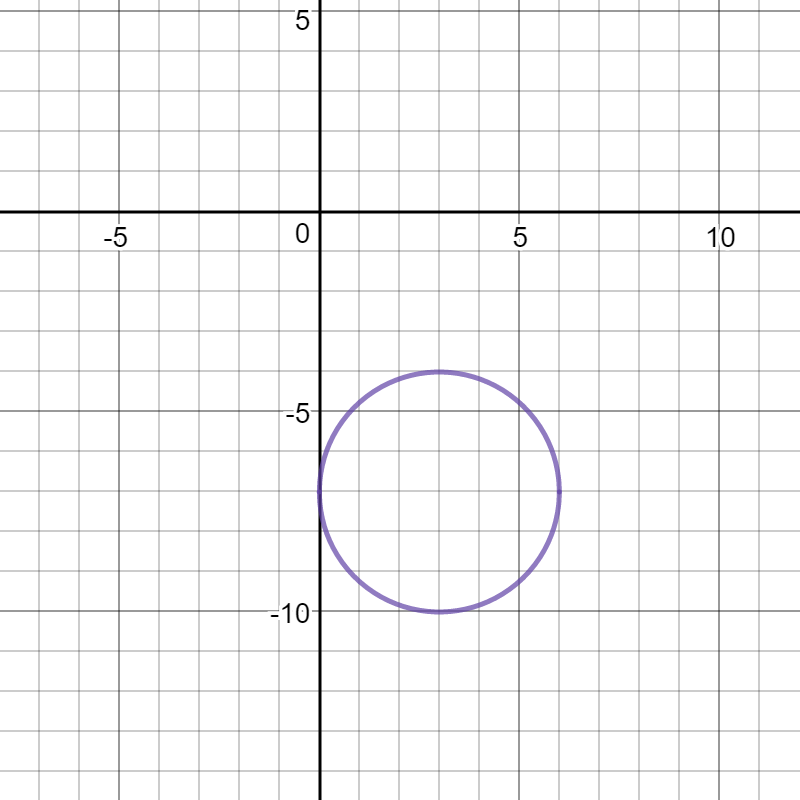
Using the general equation of a circle, set up the translations accordingly, then with a point on the
Explanation:
The equation of a circle in the center is
The center can be translated by subtracting from the
If it had a radius of

Now, as for the radius, and the circle being tangent to the y-axis. This means it has to touch the
Thinking about the center of the circle, and perhaps the figure above, as we expand the radius, the first point that touches the
Why don't we plug that into the equation we already have, and solve for
And simplify:
That makes sense algebraically, but since this is a geometric figure, radii are positive:
Plugging that back in to our equation:
And here's what it looks like:

Indeed, the center is at
Explanation:
The reqd. circle touches the
From Geometry, we know that, the
Centre to the tangent line equals radius
Now, the
Hence, the eqn. follows :


