How do you write the solution in interval notation, and graph #-5/3x<=-10#?
1 Answer
Feb 17, 2018
Interval notation:
See the graph below.
Explanation:
First, solve for x:
When dividing or multiplying by a negative, then flip the inequality sign.
To write interval notation, use brackets
In this case, the answer is included. The answer also goes up to infinity, which will always have a parenthesis, as you cannot reach infinity:
This means that any number from
A graph would look like this:
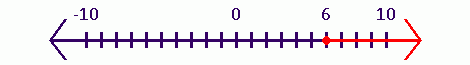
The dot at 6 is shaded in as 6 is included in the answer.

