Question

How do you write the standard form of the equation of the circle with the given the center (7,-3); tangent to the x-axis?

Answer 1

`(x-7)^2+(y-(-3))^2= 3^2` (explicit standard circle format)
or `(x-7)^2+(y+3)^2=9` (implicit standard circle format)
or `x^2+y^2-14x+6y+49` (standard polynomial format for an equation that happens to be a circle).

Explanation:

If the circle has a center at `(7,-3)` and is tangent to the X-axis
then it has a radius of `r=3`

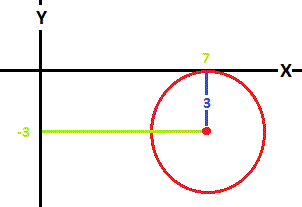
The explicit standard circle equation for a circle with center at `(x_c,y_c)` and radius `r` is
`color(white)("XXX")(x-x_c)^2+(x-y_c)^2=r^2`
which given the first version above `(x-7)^2+(y-(-3))^2=3^3`

Some (but not all) teachers like to see this expanded to get rid of the double minus signs and express the squared radius as a single entity:
`color(white)("XXX")(x-7)^2+(y+3)^3=9`

and still others are looking for the standard form of a general polynomial which is completely expanded with the right side as a series of terms in decreasing degree and the left side `=0`
(The third form above).