How does k affect Gibbs free energy?
1 Answer
It's not that
I'm going to take you literally and assume you mean the rate constant
You might see this in transition state theory, which basically says that there is a "quasi-equilibrium" between the reactant(s) and the transition state. What that means for us is that if we study the transition state, we learn more about the rate constant.
In 1889, Arrhenius proposed an equation to relate a change in energy with the rate constant:
#(dlnk)/(dT) = (DeltaE)/(RT^2)#
If we work with this a bit, we can get this to a more recognizable form.
#int dlnk = int (DeltaE)/(RT^2)dT# [after several steps...]
#color(green)(lnk = -(E_a)/(RT) + ln A# where we define
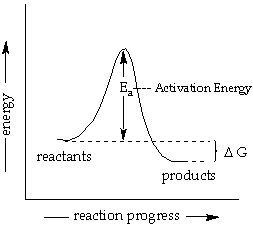
#E_a = DeltaE# as the difference between the reactant energy and the transition state energy. That is the activation energy of the reaction.#A# is the "pre-exponential factor", which basically accounts for the frequency of collisions.
We can work with this further to get to a form you may have seen in high school.
#k = e^(-(E_a)/(RT) + ln A)#
#color(blue)(k = Ae^(-E_a"/RT"))#
An analogous relation to this is:
#\mathbf(k prop e^(-DeltaG^‡"/RT"))# where
#DeltaG^‡# is the Gibbs' free energy for the transition state formation.
It is not to be confused with the
#DeltaG# given in the previous diagram, which is the Gibbs' free energy for the further reaction of the transition state to make the product(s).
From this, we can say that if the value of
The smaller the magnitude of
#DeltaG^‡# , the higher the rate constant#k# , the faster the reaction.
(As a quick example, using a catalyst lowers the activation energy, decreasing

