How fast is the water level rising when the water is 3 cm deep (at its deepest point) if water is poured into a conical container at the rate of 10 cm3/sec. the cone points directly down, and it has a height of 25 cm and a base radius of 15 cm?

Question

23148 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-02-25T23:06:20

Given the rate of change in volume with respect to time is
#(d V) / dt = 10 ##(cub. cm)/(sec)#

We are looking for the rate of change in height with respect to time:
#(d h) / dt#

#(d V)/(dt) * ( ? ) = (d h)/(dt)#

The obvious replacement for #( ? )# would seem to be
#(d h)/(dV)#, the rate of change in height with respect to Volume.

The volume of a cone is given by the formula:
#V = (Pi r^2 h)/3#

The ratio of the radius to the height for the given cone is
#r/h = 15/25 = 3/5# (see diagram)

or
#r = 3/5 h#
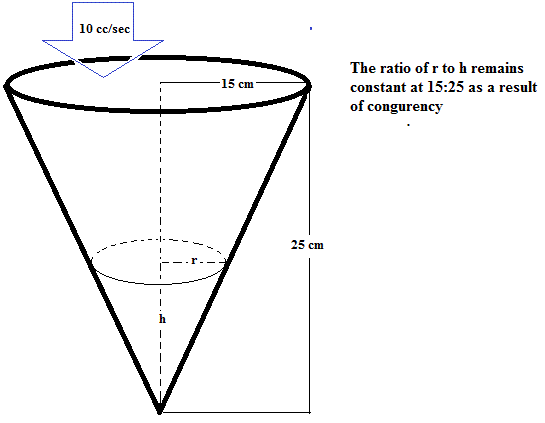
enter image source here

So, for the given cone:
#V = (Pi * (3/5 h)^2* h)/3 = (3 Pi h^3)/25 (cub. cm)#

Therefore
#(d V)/(dh) = (9 Pi)/(25) h^2 (sq. cm)#

#rarr (d h)/(dV) = (25)/( 9 Pi h^2 (sq. cm))#

#(d h)/(dt)#
#=(d V)/(dt) * (d h)/(dV) = (10 cub. cm)/(sec) * (25)/(9 Pi h^2 (sq. cm))#
#= (250 cm)/(9 Pi h^2 sec)#

at h=3
#(d h)/(dt)# becomes
#(250)/(9 Pi xx (9)) ((cm)/(sec))#

# = (250/(81 * Pi)) ((cm)/(sec))#