How is average velocity related to the secant line?
1 Answer
Well, this is a very good question indeed!
To understand this you must think first at the motion with uniform velocity and its graphical representation.
Consider a car that is traveling with constant velocity (acceleration a = 0). The car moves of the same distance at each second. You can "see" the distance vs time in a graph:
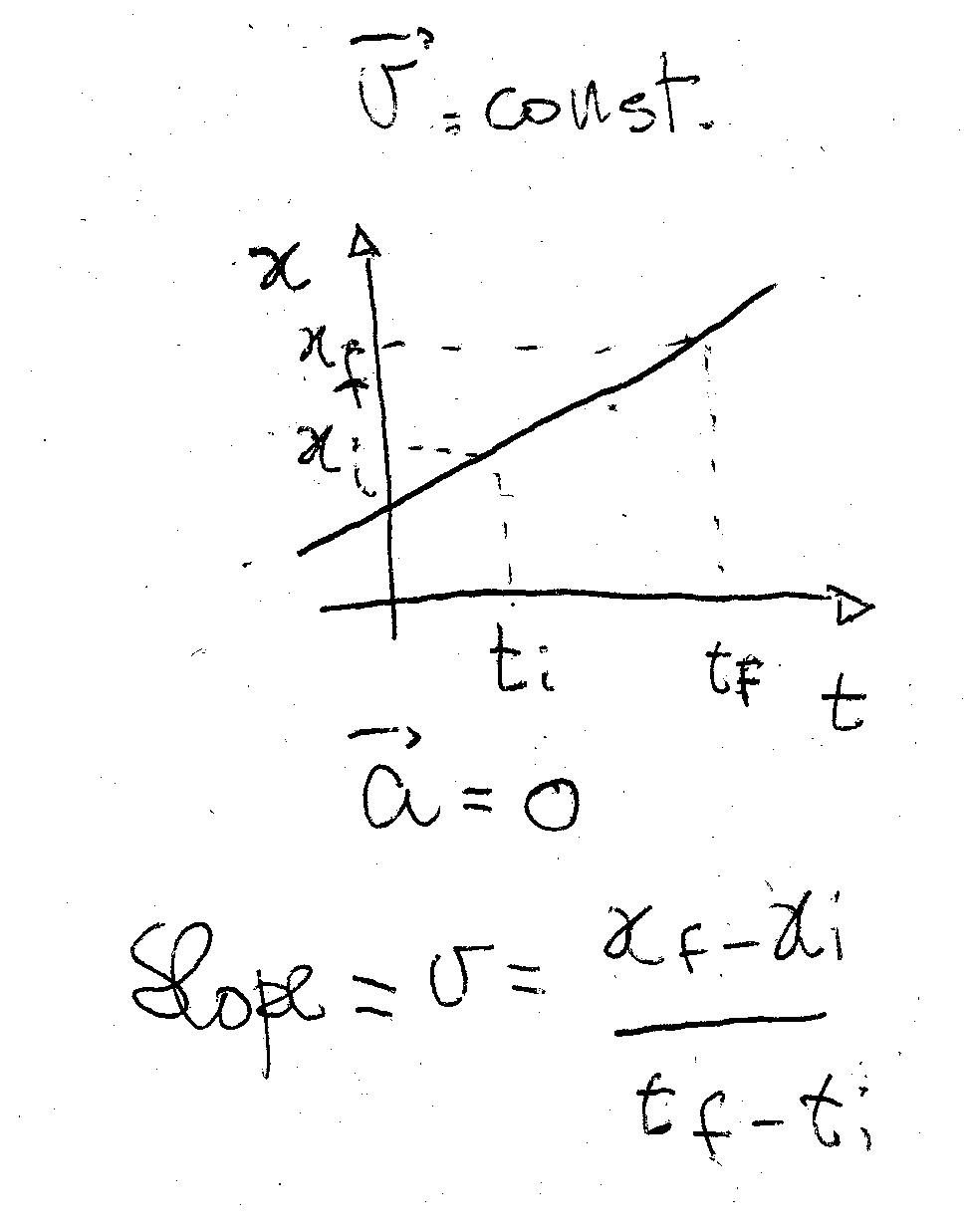
The slope of the line representing the time dependence of distance is your constant velocity.
Now, if your velocity is changing, you have acceleration and the curve in your distance vs time graph cannot be a straight line because your car will describe diferent distances at each second during its motion!!!

In our graph the car is slowing down but what is its velocity?
It is very difficult to evaluate the velocity of the car (because it is continuously changing) but you can try to evaluate an estimate of the velocity, an average velocity.
You take two points A and B and put a line through them, a secant. This is similar to the line in the first graph so that the slope of this line will be the new velocity, the average velocity!!!
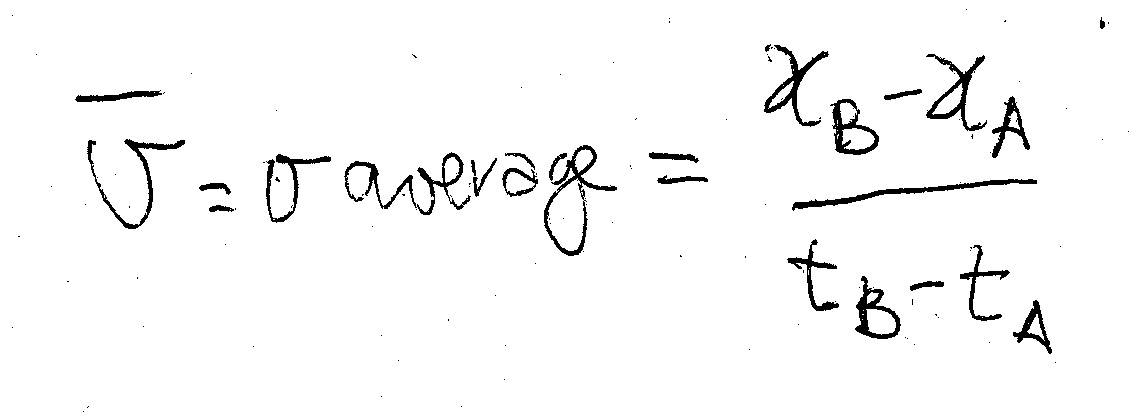
Obviously you do not know or decide to ignore what happens to the velocity in the middle of A and B.

