Average Velocity
Key Questions
-
Answer:
See below.
Explanation:
It depends on the nature of the motion you're studying. For example, if a body moves with constant velocity, you will have
#v=s/t# , and#a=0# .
On the other hand, if a body moves with constant acceleration, you will have#v = at# and#a = k# (some constant).In general, the only thing you can say is that, if you know the function
#s(t)# that gives the position#s# at every time#t# , you will have that the velocity is the first derivative of#s# , and the acceleration the second derivative. -
Average velocity = total distance / total time
Example:
I travel from Rotterdam to Amsterdam (100 km) with an average speed of 80 km/h and return with an average speed of 120 km/h.Then my average verlocity is NOT 100 km/h, but:
Time for the trip out:
#(100km)/(80km//h)=1.25h# Time for the trip back:
#(100km)/(120km//h)~~0.83h# Total time:
#1.25+0.83=2.08h# over#200 km# Average velocity:
#200/2.08=96.0km//h# This may be counter-intuitive, but remember you spend more time in the slow mode than in the fast mode.
-
Answer:
See below:
Explanation:
Common calculus problems involve displacement-time functions,
#d(t)# . For the sake of the argument let's use a quadratic to describe our displacement function.#d(t)=t^2-10t+25# Velocity is the rate of change of displacement- the derivative of a
#d(t)# function yields a velocity function.#d'(t)=v(t)=2t-10# Acceleration is the rate of change of velocity- the derivative of a
#v(t)# function or the second derivative of the#d(t)# function yields an acceleration function.#d''(t)=v'(t)=a(t)=2# Hopefully, that makes their distinction clearer.
-
Answer:
The average velocity is the displacement divided by time
Explanation:
The average velocity takes the form
#v_(av)=(x_2-x_1)/(t_2-t_1)# The displacement of a moving object is defined as the vector distance from an intial point to the final point.
-
Well, this is a very good question indeed!
To understand this you must think first at the motion with uniform velocity and its graphical representation.Consider a car that is traveling with constant velocity (acceleration a = 0). The car moves of the same distance at each second. You can "see" the distance vs time in a graph:
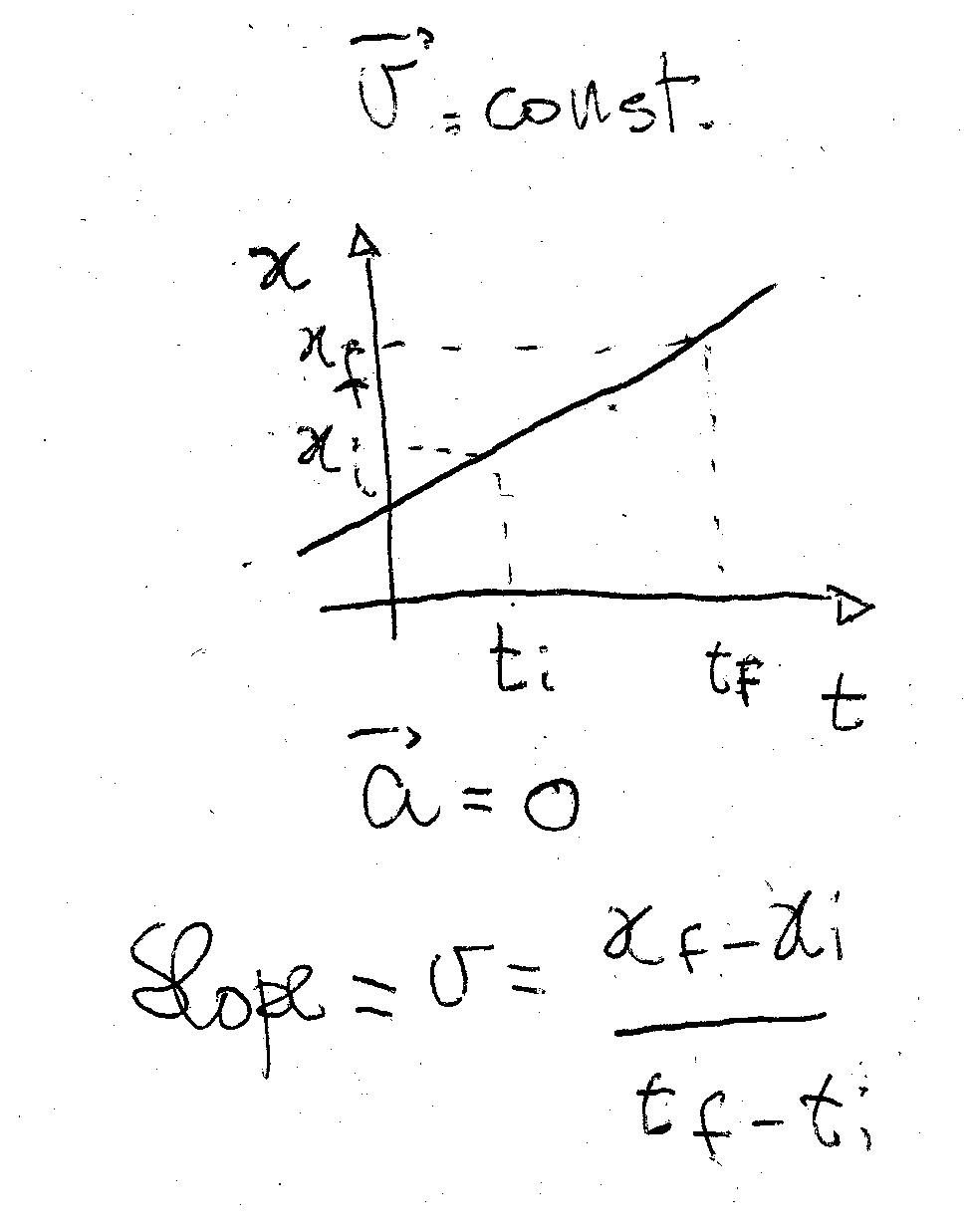
The slope of the line representing the time dependence of distance is your constant velocity.Now, if your velocity is changing, you have acceleration and the curve in your distance vs time graph cannot be a straight line because your car will describe diferent distances at each second during its motion!!!
In our graph the car is slowing down but what is its velocity?
It is very difficult to evaluate the velocity of the car (because it is continuously changing) but you can try to evaluate an estimate of the velocity, an average velocity.You take two points A and B and put a line through them, a secant. This is similar to the line in the first graph so that the slope of this line will be the new velocity, the average velocity!!!
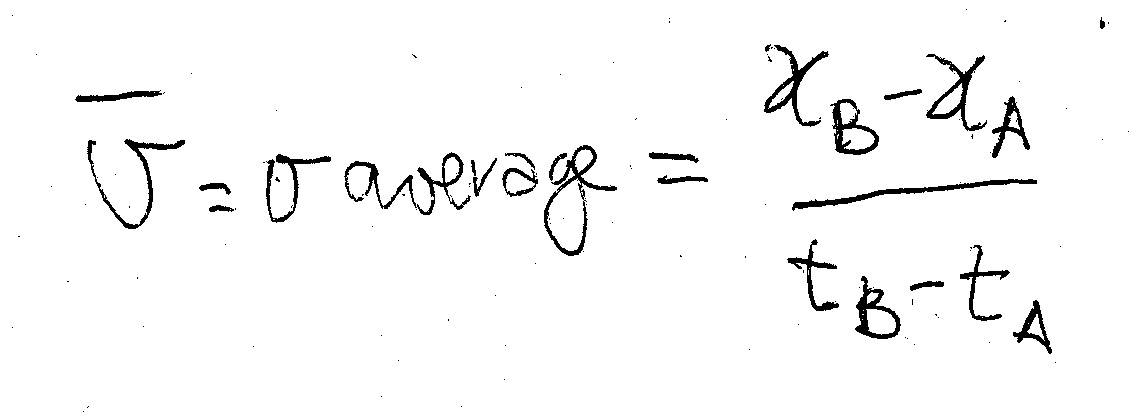
Obviously you do not know or decide to ignore what happens to the velocity in the middle of A and B.
