Let us say that we expect a linear relation, say #y=ax+b#, between two observable variables #x# and #y# and where #a# and #b# are not known. It is not necessary that the relation should be linear, but here we have assumed this only for the purpose of simplification.
However, actual observed data may be accompanied by errors or noise for various reasons and when we plot the observed data on a graph, it may not be a linear and may be some thing as shown below.
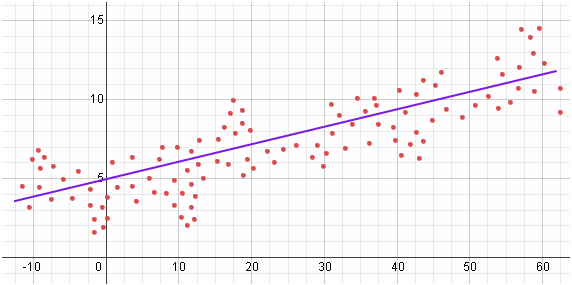
Observe that each point denotes observed value of #x# and #y# and #n# points provides us with #n# data points given by #(x_i,y_i)#, where #i# ranges from #1# to #n#.
We can draw many lines through these points, with varying slopes i.e. #a's# and intercepts #b's#, but how do we know which one is the best fit. This is done by the method of Least squares. In this method we define the relationship between observed data and expected data - by minimizing the sum of squares of the deviation between observed and expected values.
In other words, best line has minimum error between line and data points. Note that had we not squared, positive and negative errors would have almost cancelled out. We will talk more about this later.@
For a particular #x_i# observed value is #y_i#, expected value of #y_i# for is #ax_i+b# and difference between them #d_i# is given by #y_i-ax_i-b# and in least square method we seek to
minimise error #E=sum_(i=1)^nd_i^2# i.e. #sum_(i=1)^n(y_i-ax_i-b)^2#.
To get this minimum, we use calculus. For this, we must have first derivatives of #a# and #b# yielding zero. Differentiating #sum_(i=1)^n(y_i-ax_i-b)^2# w.r.t. #a# and #b#, we get
#(delE)/(dela)=-2sum_(i=1)^nx_i(y_i-ax_i-b)=0#
and #(delE)/(delb)=-2sum_(i=1)^n(y_i-ax_i-b)=0#
To solve for #a# and #b#, we rewrite them as
#asumx_i^2+bsumx_i=sumx_iy_i# and
#asumx_i+bn=sumy_i#
and solving them for #a# and #b# we get
#a=(sumy_isumx_i^2-sumx_isumx_iy_i)/(nsumx_i^2-(sumx_i)^2)#
and #b=(nsumx_iy_i-sumx_isumy_i)/(nsumx_i^2-(sumx_i)^2)#
@ - Note that #asumx_i+bn=sumy_i# can be expressed as #asumx_i/n+b=sumy_i/n# is just a fit between averages of #x_i# and #y_i#. Hence, this alone may not give the best fit. The latter is arrived due to #asumx_i^2+bsumx_i=sumx_iy_i#.

