Question

How many electrons in an atom can have `n + l =6` ?

The answer is 18. How do you get this answer?? Thanks!

Answer 1

`"18 e"^(-)`

Explanation:

As you know, we use four quantum numbers to describe the location and spin of an electron in an atom.

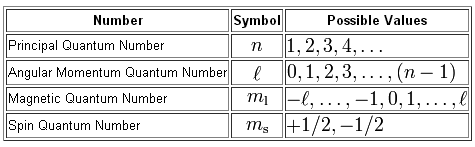
In your case, you must find the number of electrons that can have

`n + l = 6" " " "color(orange)("(*)")`

The angular momentum quantum number, `l`, which tells you the subshell in which the electron is located, depends on the value of the principal quantum number, `n`, which tells the energy level on which the electron resides, as given by

`l <= n-1`

Right from the start, you can tell that the first energy level that can hold electrons that satisfy condition `color(orange)("(*)")` corresponds to `n=4`, since for

`n = 3 implies l = (0, 1, 2}`

you can't have a pair that matches the given condition

• `3 + 0 < 6" "color(red)(xx)`

• `3 + 1 < 6" "color(red)(xx)`

• `3 + 2 < 6 " "color(red)(xx)`

The same is true, of course, for `n=1` and `n=2`.

Now, for `n=4` you have

`n = 4 implies l = {0, 1, 2, 3}`

`4 + 2 = 6" "color(green)(sqrt())`

For the angular momentum quantum number, you have

• `l=0 ->` the s-subshell
• `l=1 ->` the p-subshell
• `l=2 ->` the d-subshell

The d-subshell holds a total of `5` orbitals as given by the magnetic quantum number, `m_l`, which in this case can take the values

`m_l = {-2, -1, 0, 1, 2} ->` for the d-subshell

Now, each orbital can hold a maximum of two electrons, which means that a total of

`5 color(red)(cancel(color(black)("d-orbitals"))) * "2 e"^(-1)/(1color(red)(cancel(color(black)("orbital")))) = "10 e"^(-)`

can have `n=4` and `l=2`. Now move on to `n=5`, for which

`n=5 implies l = {0, 1, 2, 3, 4}`

This time, you can have

`5 + 1 = 6" "color(green)(sqrt())`

The p-subshell holds a total of `3` orbitals as given by `m_l`

`m_l = {-1,0,1} ->` for the p-subshell

Each of those orbitals can hold `2` electrons, so

`3 color(red)(cancel(color(black)("p-orbitals"))) * "2 e"^(-)/(1color(red)(cancel(color(black)("orbital")))) = "6 e"^(-)`

can have `n=5` and `l=1`. Finally, move on to `n=6`, for which

`n=6 implies l = {0,1,2,3,4,5}`

This time, you have

`6 + 0 = 6" "color(green)(sqrt())`

The s-subshell holds a single orbital, since

`m_l = 0 ->` for the s-subshell

This means that only

`1 color(red)(cancel(color(black)("s-orbital"))) * "2 e"^(-)/(1color(red)(cancel(color(black)("orbital")))) = "2 e"^(-)`

can have `n=6` and `l=0`.

Therefore, the total number of electrons that can have `n+l = 6` will be

`overbrace("10 e"^(-))^(color(blue)(4 + 2 = 6)) + overbrace("6 e"^(-))^(color(darkgreen)(5 + 1 = 6)) + overbrace("2 e"^(-))^(color(purple)(6 + 0 = 6)) = "18 e"^(-)`