How many hydroxide ions are needed to completely neutralize 1.0 liter of 0.50 M HCl?
1 Answer
Explanation:
The idea here is that the hydronium cations,
In other words, it takes
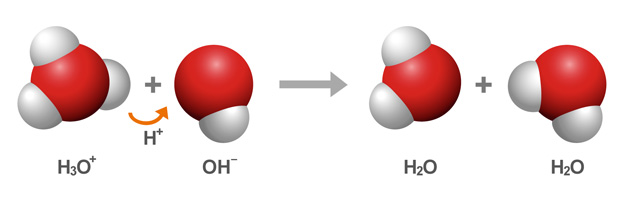
Now, you know that you're dealing with
Since hydrochloric acid is a strong acid, it will ionize completely in aqueous solution to produce hydronium cations
#"HCl"_ ((aq)) + "H"_ 2"O"_ ((l)) -> "H"_ 3"O"_ ((aq))^(+) + "Cl"_ ((aq))^(-)#
This means that your solution contains
As a result, you can say that you will need
Now, to convert this to the number of anions, you need to use Avogadro's constant, which tells you that in order to have
Therefore, you will need
#0.50 color(red)(cancel(color(black)("moles OH"^(-)))) * (6.022 * 10^(23)color(white)(.)"OH"^(-)"anions")/(1color(red)(cancel(color(black)("mole OH"^(-))))) = color(darkgreen)(ul(color(black)(3.0 * 10^(23)color(white)(.)"OH"^(-)"anions"#
to completely neutralize
The answer is rounded to two sig figs.

