Step 1. Write the balanced chemical equation.
The balanced equation is
#"2KClO"_3 → "2KCl" + "3O"_2#
Step 2. Strategy
The problem is to convert grams of #"KClO"_3# to millilitres of #"O"_2#.
We can use the flow chart below to help us.
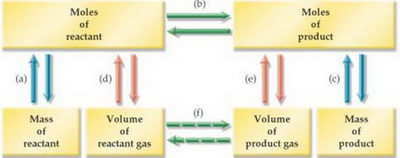
(Adapted from www.lsua.us)
The process is:
(a) Use the molar mass to convert mass of #"KClO"_3# to moles of #"KClO"_3#.
(b) Use the molar ratio (from the balanced equation) to convert moles of #"KClO"_3# to moles of #"O"_2#.
(e) Use the Ideal Gas Law to convert moles of #"O"_2# to volume of #"O"_2#.
In equation form,
#"grams of KClO"_3 stackrelcolor(blue)("molar mass"color(white)(ml)) (→) "moles of KClO"_3 stackrelcolor(blue)("molar ratio"color(white)(ml))→ "moles of O"_2 stackrelcolor(blue)("Ideal Gas Law"color(white)(ml))(→) "volume of O"_2#
The Calculations
(a) Moles of #"KClO"_3#
#0.300 color(red)(cancel(color(black)("g KClO"_3))) × ("1 mol KClO"_3)/( 122.55 color(red)(cancel(color(black)("g KClO"_3)))) = "0.002 448 mol KClO"_3 #
(b) Moles of #"O"_2#
#0.002 448color(red)(cancel(color(black)("mol KClO"_3))) × ("3 mol O"_2)/(2 color(red)(cancel(color(black)("mol KClO"_3)))) = "0.003 672 mol O"_2#
(c) Volume of #"O"_2#
The Ideal Gas Law is
#color(blue)(|bar(ul(color(white)(a/a)PV = nRTcolor(white)(a/a)|)))" "#
We can rearrange this to give
#V = (nRT)/P#
#n = "0.003 672 mol"#
#R = "0.082 06 L·atm·K"^"-1""mol"^"-1"#
#T = "(25 + 273.15) K" = "298.15 K"#
#P = 755 color(red)(cancel(color(black)("mmHg"))) × "1 atm"/(760 color(red)(cancel(color(black)("mmHg")))) = "0.9934 atm"#
∴ #V = ("0.003 672" color(red)(cancel(color(black)("mol"))) × "0.082 06"color(white)(l) "L"·color(red)(cancel(color(black)("atm·K"^"-1""mol"^"-1"))) × 273.15color(red)(cancel(color(black)( "K"))))/(0.9934 color(red)(cancel(color(black)("atm")))) = "0.0829 L" = " 82.9 mL"#
The volume of #"O"_2# produced is #"82.9 mL"#.


