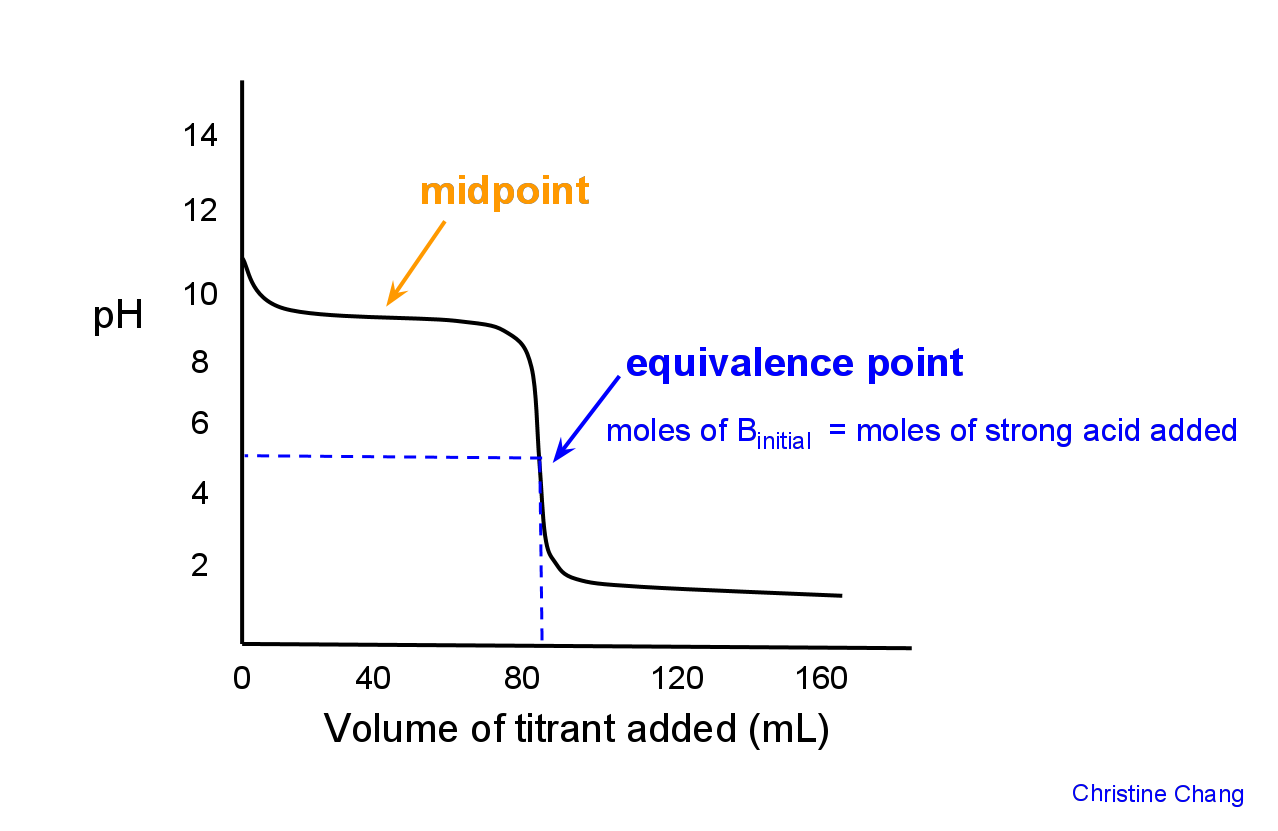
How many moles of HX have been added at the equivalence point?
Assume that 30.0 mL of a 0.10 M solution of a weak base B that accepts one proton is titrated with a 0.10 M solution of the monoprotic strong acid HX.
Assume that 30.0 mL of a 0.10 M solution of a weak base B that accepts one proton is titrated with a 0.10 M solution of the monoprotic strong acid HX.
1 Answer
Explanation:
You're titrating a weak base
That is what you're looking for here -- the number of moles of strong acid needed to completely neutralize the weak base. This is what the equivalence point is.
So, the balanced chemical equation for this reaction can be written like this
#"B"_ ((aq)) + "HX"_ ((aq)) -> "BH"_ ((aq))^(+) + "X"_((aq))^(-)#
So, if every mole of weak base requires
You know that both solutions have a molarity of
All you have to do now is use the molarity of the strong acid solution as a conversion factor to find the number of moles of
A
#30.0 color(red)(cancel(color(black)("mL"))) * (1color(red)(cancel(color(black)("L"))))/(10^3color(red)(cancel(color(black)("mL")))) * "0.10 moles HX"/(1color(red)(cancel(color(black)("L")))) = color(green)(|bar(ul(color(white)(a/a)color(black)("0.0030 moles HX")color(white)(a/a)|)))#
The answer is rounded to two sig figs.
SIDE NOTE Notice that the neutralization reaction produces
This tells you that the pH at equivalence point will actually be lower than