How many points of inflection does the function #f(x)=x^7-x^2# have?
1 Answer
Explanation:
Inflection points are where the function changes concavity.
The second derivative must equal zero when the function changes concavity.
But we must check points on either side to make sure that the concavity really does change.
So,
To make sure that the concavity actually changes, we pick a number on either side of
Let's use
The concavity changes, so
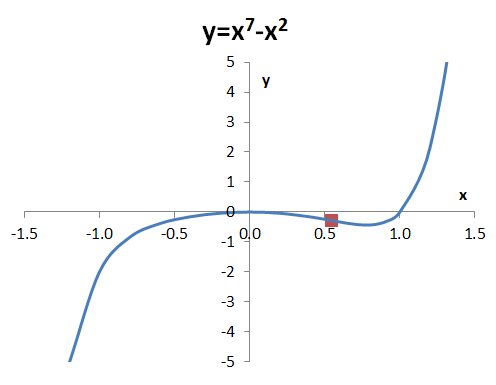
The brown square represents the inflection point.

