How many real solutions do the equation #sin(e^x)-5^x-5^(-x)=0# have? Thank you!
1 Answer
No real solutions.
Explanation:
The equation is
with
The equation
You can obtain complex roots proceeding as follows.
(1) Define the complex function
(2) Determine the real and imaginary components. In this case we have
(3) Using an iterative procedure such as Newton-Raphson, determine the solutions for
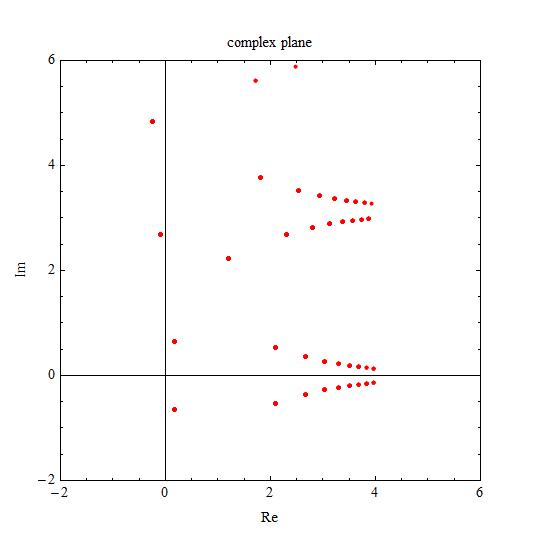
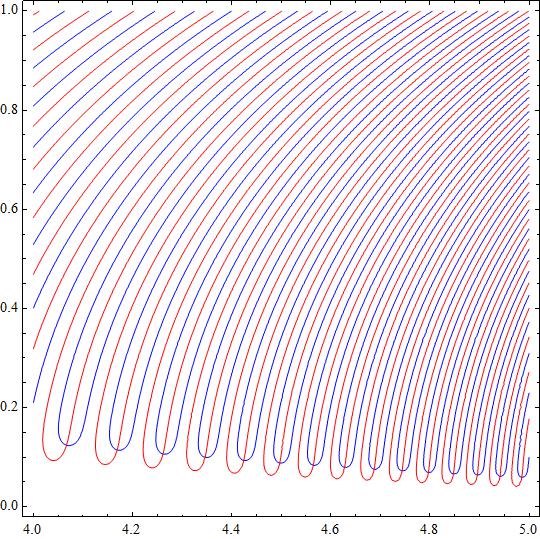
To have an idea about the roots placement there is an attached plot showing in blue the contour for
The complex roots lay into the intersection of both curves.
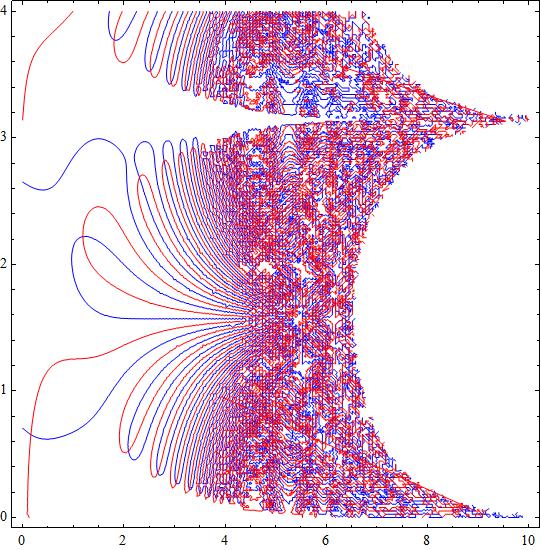
and a zoomed region
A sample of solutions