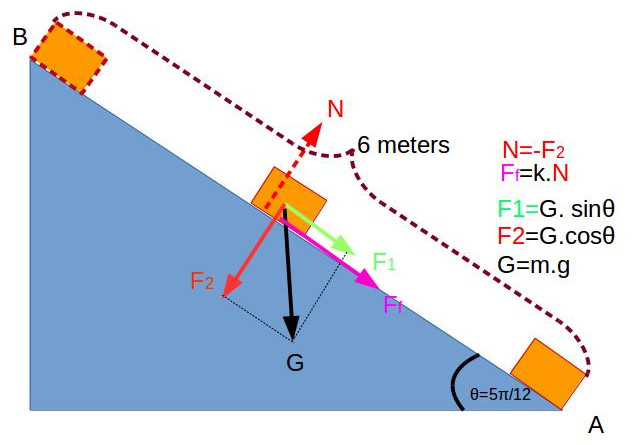
#step:1#
#"let's convert radian to degree"#
#theta=180*(5cancel(pi))/(12cancel(pi))=75^o#
#sin 75=0,966 #
#cos 75=0,259#
#G=m*g=1*9,81=9,81N#
#step:2#
#color(green)(F_1)=G*sin theta=9,81*0,966=9,47616N#
#color(red)(F_2)=G*cos theta=9,81*0,259=2,54079N#
#color(red)(N=-F_2)=-2,54079N#
#color(red)(N) "is the reacting force to" color(red)(F_2)"by acting surface" #
#color(purple)(F_f)=k*color(red)(N)"(friction force)"#
#color(purple)(F_f)=4*2,54079=10,16316N#
#"now let's sum these forces"#
#sumF=color(green)(F_1)+color(purple)(f_f)#
#sumF=9,47616+10,16316#
#sumF=19,63932N#
#step:3#
#sumF" is the minimum force that will transport object from" #
#"the point A to the point B"#
#W=sumF* Deltax#
#W=19,63932*6#
#W=117,83592# "Joule"

