The first step in solving this problem is to identify the forces acting on the object and determine which among them are doing work on it.
Here is a free-body diagram:
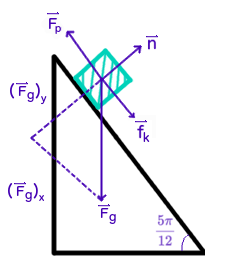
Where F_p represents the force of the push, n is the normal force, f_k is the force of kinetic friction, and F_(gx) and F_(gy) are the horizontal and vertical components of the force of gravity, respectively.
Note : force vectors and angle are not drawn to scale.
Work is done by the component of the force parallel to displacement, and so, as a rule, forces which act perpendicular to the motion of the object do no work.
The normal force is an example of this. If an object is on a level, horizontal surface, the force of gravity does no work. If we look at the equation for work, W=FΔrcos(theta), we can see that a force acting at a 90^o angle relative to the motion of the object would produce a work of 0, as cos(90^o)=0. If the object were moving vertically, the force of gravity would do work on an object. Because our object is on an incline, the force of gravity has both perpendicular and parallel components, and it is the parallel component which does work.
Therefore, the forces which do work on the object are those of friction, the push, and the parallel component of gravity. The net work will be the sum of each of these individual works.
W=W_F+W_P+W_(Gx)
However, since we know that the forces of gravity and friction work against the motion, they are assigned negative values, and so we have
W=W_P-W_F-W_(Gx)
We want to determine the work done by the push, so we can solve for W_P
W_P=W_F+W_(Gx)
Thus, we need to calculate the work done by friction and the parallel component of the force of gravity to get our answer.
The work done by friction is given by W_F=f_kΔrcos(theta), and the work done by gravity is given by W_(Gx)=F_(Gx)Δrcos(theta). In the equation for work, theta is the angle between the force and displacement vectors. Because both friction and the horizontal component of gravity are acting parallel to the displacement of the object but in the opposite direction, theta is 180^o. Therefore, work done in the opposite direction of displacement is negative (cos(180^o)=-1), and that in the same direction as displacement is positive (we already took this into account above).
The force of kinetic friction is given by f_k=mu_kn, so we need to determine the normal force in order to calculate f_k. From the force diagram above, we can see that n=F_(Gy)=mgcos(theta). In this equation, theta is the angle at which the force of gravity is acting to produce the parallel component, different from the theta used above in the equation for work.
W_F=mu_kmgcos(theta)Δr
We can also determine an expression for the parallel component of gravity using the force diagram. F_(Gx)=mgsin(theta).
W_(Gx)=mgsin(theta)Δr
And so,
W_P=mu_kmgcos(theta)Δr+mgsin(theta)Δr
Using our known values:
W_P=(2)(4kg)(9.8m/s^2)cos((5pi)/12)(9m)+(4kg)(9.8m/s^2)sin((5pi)/12)(9m)
W_P=523J
Note that 2 is a large coefficient of friction. Typically these values are less than 1, though some materials can have values larger than this. A coefficient of 1 implies that the frictional force is equal to the normal force.


