Question

How much work does it take to push an object with a mass of `6 kg` up a `1 m` ramp, if the ramp has an incline of `(5pi)/12` and a kinetic friction coefficient of `7`?

Answer 1

The work is `=163.3J`

Explanation:

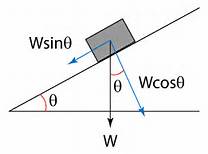
The coefficient of kinetic friction is

`mu_k=F_r/mgcostheta`

`F_r=mu_kmgcostheta`

The mass is m=6kg#

The coefficient of kinetic friction is `mu_k=7`

The angle is `theta=5/12pi`

The distance is `d=1m`

Resolving in the direction parallel to the plane `↗^+`

The force is

`F=mgsintheta+mu mgcostheta`

The work is

`W=Fd`

`=(mgsintheta+mu mgcostheta)*d`

`=mg(sintheta+mu_kcostheta)*d`

`=6g(sin(5/12pi)+7cos(5/12pi))*1`

`=163.3J`