How much work would it take to push a # 1 kg # weight up a # 6 m # plane that is at an incline of # pi / 3 #?
1 Answer
Explanation:
Work done by a constant force is given as the dot product of the force and displacement vectors:
#color(blue)(W=Fdcostheta)#
- Where
#theta# is the angle between the force and displacement vectors. This is not the angle of incline.
Diagram:
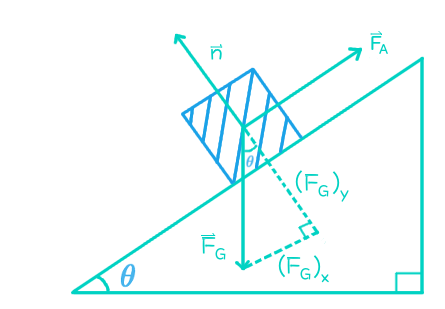
-
Where
#vecF_A# is the applied (pushing) force,#vecn# is the normal force, and#vecF_g# is the force of gravity, broken up into its parallel (x, horizontal) and perpendicular (y, vertical) components. -
I will define up the incline as positive
We can use Newton's second law to determine the net force on the object.
#color(blue)(F_(x" net")=sumF_x=F_A-F_(Gx)=ma_x)#
#color(blue)(F_(y" net")=sumF_x=n-F_(Gy)=ma_y)#
- We will assume dynamic equilibrium, as it is assumed that we are looking for the minimum amount of work required to push the object up the incline.
#=>F_A-F_(Gx)=0#
#=>n-F_(Gy)=0#
Which gives:
#=>color(blue)(F_A=F_(Gx))#
#=>color(blue)(n=F_(Gy))#
Therefore, the magnitude of the pushing force required is equal to the parallel component of the force of gravity. We can find this component using our diagram and basic trigonometry.
#=>sin(theta)="opposite"/"hypotenuse"#
#=>sin(theta)=F_(Gx)/F_G#
#=>F_(Gx)=F_Gsin(theta)#
And as we know that
#=>color(blue)(F_(Gx)=mgsin(theta))#
Finally, we have:
#F_A=mgsin(theta)#
Putting this into the equation for work:
#W=mgsin(theta_i)dcos(theta)#
Since the pushing force is in the same direction as the displacement (up the ramp),
#W=mgsin(theta)d#
We have the following information:
#|->m=1"kg"# #|->d=6"m"# #|->theta_i=pi/3# #|->g=9.81"m"//"s"^2#
#=>W=(1"kg")(9.81"m"//"s"^2)(6"m")sin(pi/3)#
#=>color(blue)(W~~51"J")#

