How much work would it take to push a # 16 kg # weight up a # 5 m # plane that is at an incline of # pi / 6 #?
1 Answer
Explanation:
Step 1:
Based on this particular problem, the free body diagram should be drawn as seen below:
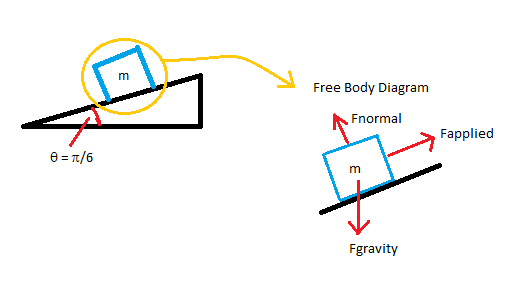
In the diagram, three forces are acting on the block:
- Gravity - always acts toward Earth
- Normal force - always acts against the object in question, perpendicular to the surface on which it is sitting
- Applied force - external force doing the work
Step 2:
After creating an FBD for the object in question (i.e. the blue block), an appropriate coordinate system should be chosen to eliminate as many variables as possible. For problems involving inclined planes, it is wise to orient the coordinate system such that the x-axis shares the same line of action as the applied force,
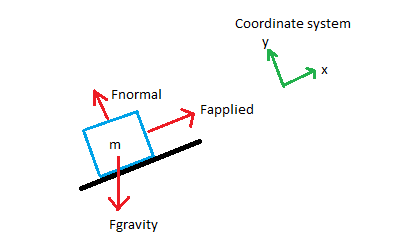
Step 3:
Since
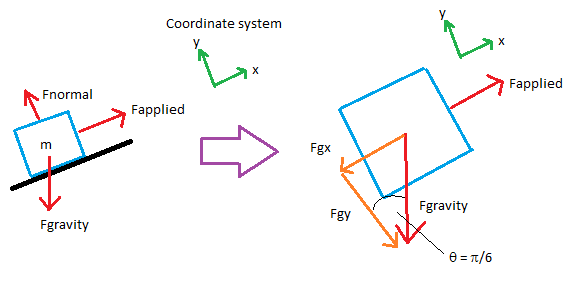
Looking at this diagram, it can be seen that
so,
Step 4:
Recall that the equation for work is

