How solve Derivatives of Trigonometric Functions?
THANK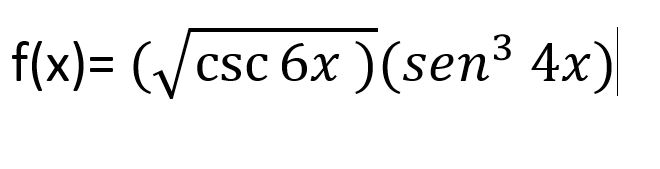 YOU
YOU
THANK YOU
1 Answer
Jun 18, 2018
Explanation:
First use the product rule:
using now the chain rule:
and as the function is defined only for

