There shouldn't be, and that's why #"B"_2# is very unstable; it has two orthogonally-localized half-#pi# bonds, which is quite a weak bond.
Imagine that each #"B"# takes the place of a #"CH"# on #"HC"-="CH"#.
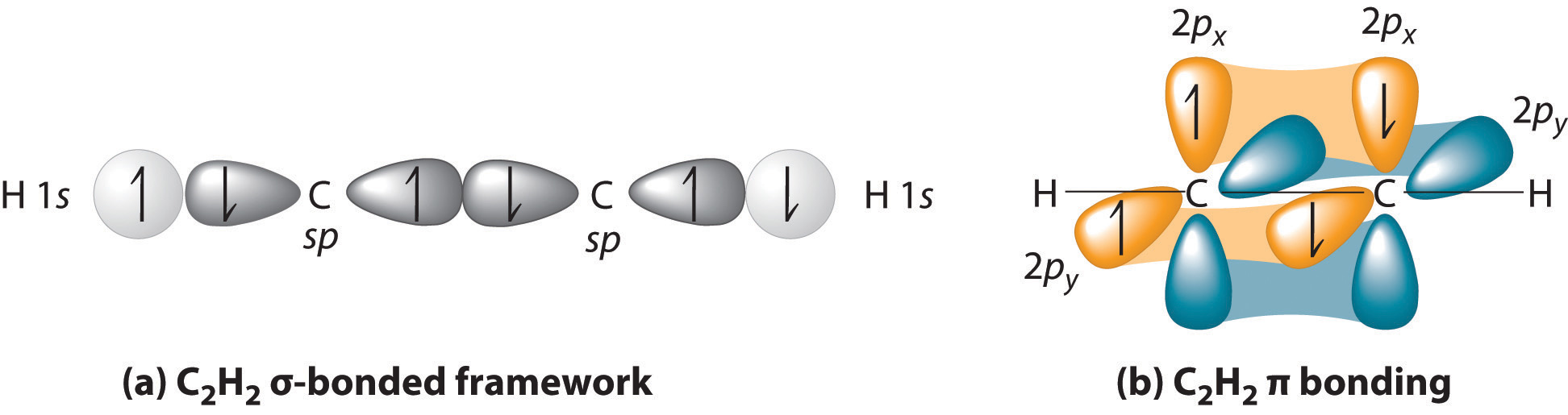
Then, take away the #sigma# bond, the two #"H"# atoms, and one electron from each of the two full #pi# bonds, and you have a structure similar to #"B"_2#.
What about #"Li"_2# "molecule"? Is that stable? (Its bond length is #"267.3 pm"#, over twice the length of an average bond.)
The first chemical bond made in a molecule is preferentially a #bbsigma# bond.
#sigma# bonds are formed from a direct atomic orbital overlap. In comparison, #pi# bonds are sidelong overlaps and thus, #sigma# overlaps are made preferentially because they form the stronger bond.
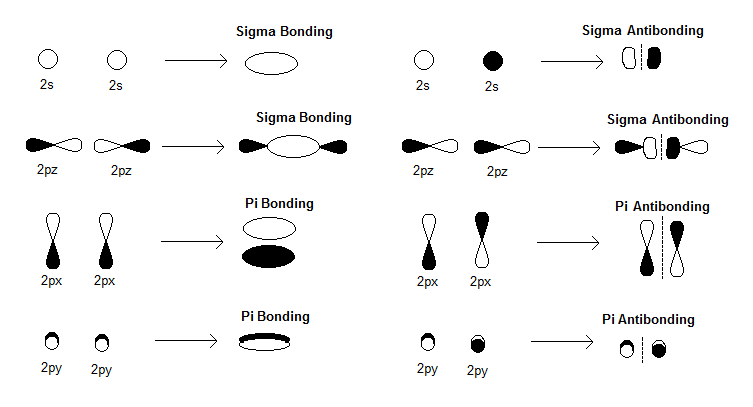
#"B"_2# contains two boron atoms, which each use a basis of a #1s#, a #2s#, and three #2p# atomic orbitals.
For #"Li"_2# through #"N"_2#, there exists an orbital mixing effect that makes the #sigma# molecular orbital for a #2p_z-2p_z# overlap (#sigma_(g(2p))#) higher in energy than the #pi# molecular orbitals for a #2p_(x//y)-2p_(x//y)# overlaps (#pi_(u(2p))#).

So, this particular orbital energy ordering takes place in the molecular orbital diagram, similar to the #"C"_2# molecule:
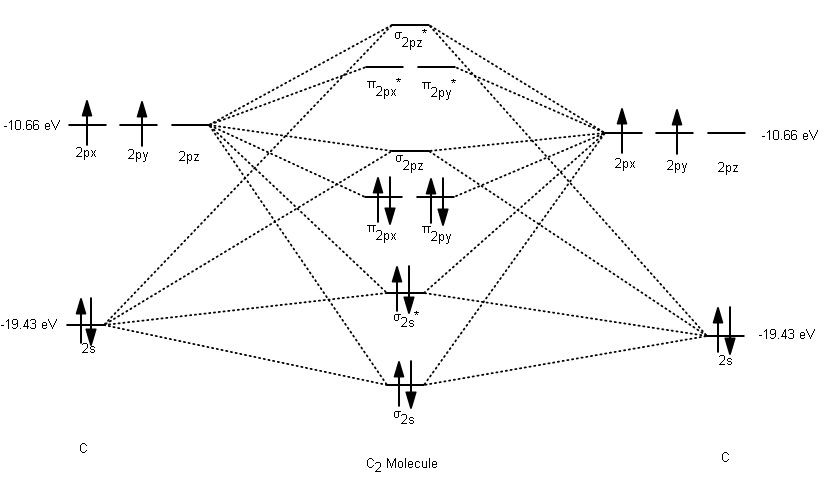
where #|E_(sigma_(2p_z))| > {|E_(pi_(2p_x))| = |E_(pi_(2p_y))|}#.
Since #"C"# has one more electron, #"B"_2# would have a similar MO diagram, EXCEPT for two fewer electrons. This, at first glance, seems to suggest that #"B"_2# has two half-#pi# bonds, with a molecular electron configuration of:
#color(green)((sigma_(1s))^2(sigma_(1s^"*"))^2(sigma_(2s))^2(sigma_(2s^"*"))^2(pi_(2p_x))^1(pi_(2p_y))^1)#
Since #"B"_2# is paramagnetic with two electrons, in order to make that bond, there are indeed two half-#bbpi# bonds, which form what we represent improperly in line notation as a #sigma# bond... and it isn't actually a #sigma# bond.
#:"B"-"B":#
That isn't a #sigma# bond, but two half-#pi# bonds. We would then expect #"B"_2# to be very unstable, which it is. (The lone pairs are from the #sigma_(2s)# and #sigma_(2s)^"*"#, since bonding + antibonding filled = nonbonding.)




