How to assign 4 quantum numbers to 2 electrons in 3p orbitals?
1 Answer
Here's how you can do that.
Explanation:
You know that we can use four quantum numbers to describe the location and the spin of an electron inside an atom.
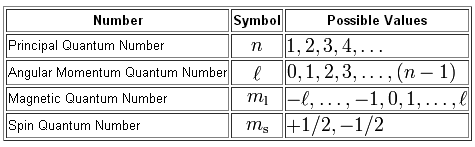
For starters, you need to know the energy level on which the electrons reside. This will give you the value of the principal quantum number,
For electrons located in a
#n = color(red)(3) -> "the third energy level"#
So, you know that you have
The
#n = 3, l =1#
Now, the
#l = 1 implies {(m_l = -1 -> "the 3p"_xcolor(white)(.)"orbital"), (m_l = color(white)(-)0-> "the 3p"_zcolor(white)(.)"orbital"), (m_l = +1-> "the 3p"_ycolor(white)(.)"orbital") :}#
Finally, the spin quantum number,
You can form several possible sets of quantum numbers to describe two electrons located in
#n = 3, l= 1, m_l = -1, m_s = + 1/2# This electron is located on the third energy level, in the
#3p# subshell, in the#3p_x# orbital, and has spin-up
#n = 3, l= 1, m_l = -1, m_s = - 1/2# This electron is located on the third energy level, in the
#3p# subshell, in the#3p_x# orbital, and has spin-down
These two sets describe electrons that are located in the same orbital, which is why the only differ in the value of the spin quantum number.
Similarly, you can have
#n = 3, l= 1, m_l = 0, m_s = + 1/2# This electron is located on the third energy level, in the
#3p# subshell, in the#3p_z# orbital, and has spin-up
#n = 3, l= 1, m_l = 1, m_s = - 1/2# This electron is located on the third energy level, in the
#3p# subshell, in the#3p_y# orbital, and has spin-down

