Question

How to calculate the density of this crystal?

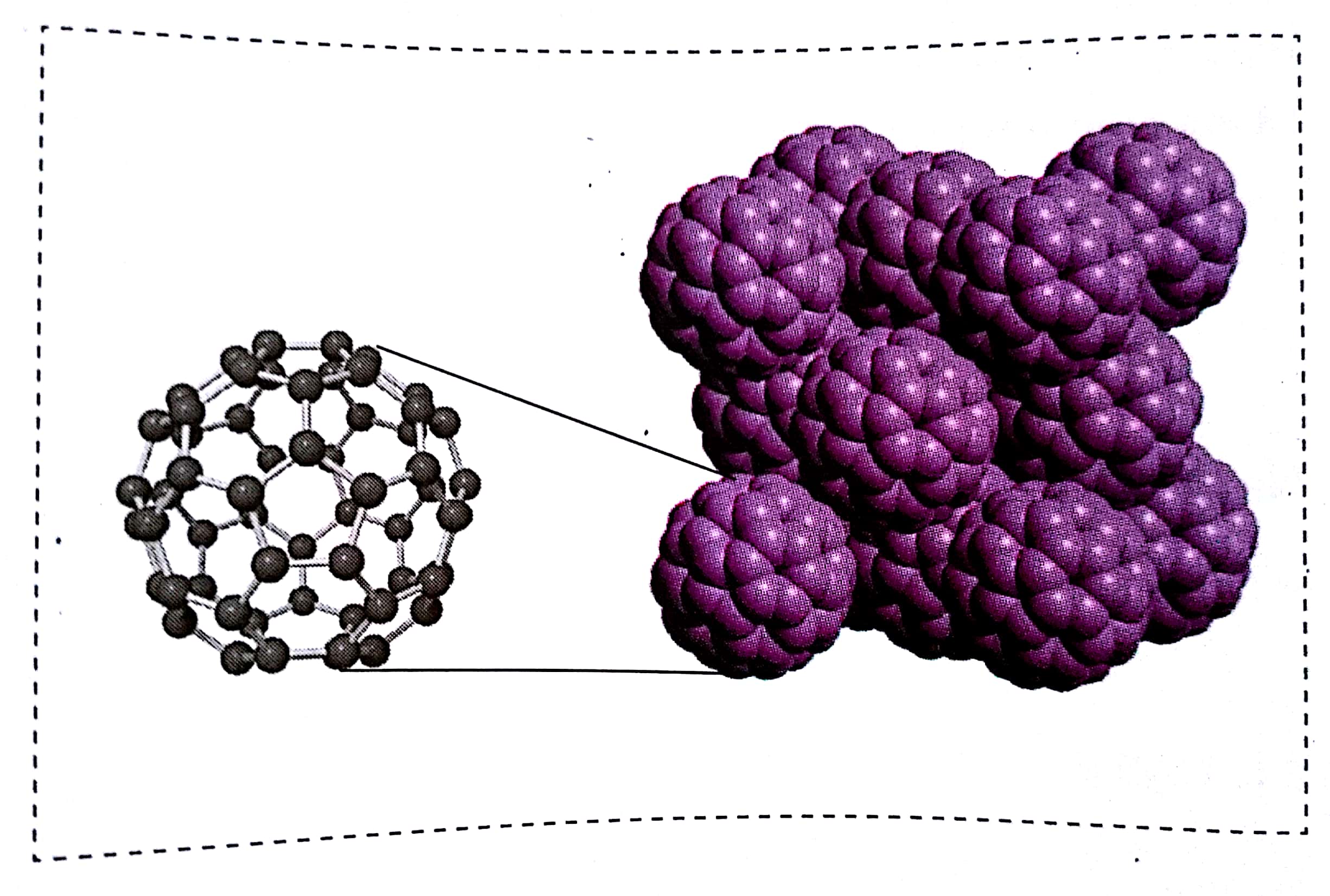
Fuleren is one of the most famous allotropic modification of carbon. The most famous is the fuleren is `C_60`. With an outer radius of 50.9 pm, sixty carbon atoms are connected to 20 hexagons and 12 spaced pentagons. This fuleren crystallizes in face-centered cubic system. How much is its density?

Answer 1

The calculated density is `"1.60 g/cm"^3`.

Explanation:

Calculate the molecules in a unit cell

The image in your question shows an fcc unit cell of fullerene.

There is ⅛ molecule at each of the 8 corners and ½ molecule at each of the six faces.

Thus, the number of molecules in a unit cell is

`"No. of molecules" = 8 color(red)(cancel(color(black)("corners"))) × "⅛ molecule"/(1 color(red)(cancel(color(black)("corner")))) + 6 color(red)(cancel(color(black)("faces"))) × "½ molecule"/(1 color(red)(cancel(color(black)("face")))) = "1 molecule + 3 molecules = 4 molecules"`

Calculate the mass of a unit cell

`"Atomic mass of C"_60 = "720.64 u"`

`"Mass of unit cell" = 4 color(red)(cancel(color(black)("molecules"))) × (720.64color(red)(cancel(color(black)("u"))))/(1 color(red)(cancel(color(black)("molecule")))) × "1 g"/(6.022 × 10^23 color(red)(cancel(color(black)("u"))))`

`= 4.787 × 10^"-21" "g"`

Calculate the edge length of a unit cell

Using Pythagoras' Theorem, we find

`d^2 + d^2 = (4r)^2`

`2d^2 = 16r^2`

`d^2 = 8r^2`

`d = rsqrt8`

I believe your radius of `"C"_60` is in error because 50.9 pm is less than the radius of a hydrogen atom.

A more reasonable value is 509 pm.

Then

`d =sqrt8 × "509 pm" = "1440 pm" = 1.440 ×10^"-9"color(white)(l) "m" = 1.440 ×10^"-7"color(white)(l) "cm"`

Calculate the volume of a unit cell

`V = d^3 = (1.440× 10^"-7"color(white)(l) "cm")^3 = 2.984 × 10^"-21"color(white)(l) "cm"^3`

Calculate the density of the unit cell

`ρ = m/V = (4.787 × 10^"-21" color(white)(l)"g")/(2.984 × 10^"-21"color(white)(l)"cm"^3) ="1.60 g/cm"^3`