A general conic has the form
#C=a x^2+b y^2+c x y + d x + e y + f=0# it can be read also as
#C = ((x),(y))((a,c/2),(c/2,b))(x,y)+(d,e)((x),(y))+f#
We know also that the kind of conic is dictated by the matrix
#M=((a,c/2),(c/2,b))#
characteristic polynomial.
#p_M(lambda)=lambda^2-2(a+b)lambda+c^2-4ab#
The ellipses are those conics for which the characteristic polynomial roots are real with same sign. We consider that the circle is a particular case of ellipse.
Keeping that in mind the condition is
#(a - b)^2 + c^2< (a+b)^2# or simplifying
#ab > (c/2)^2#
Now, substituting #p_1,p_2,p_3,p_4# into #C# we have
#{(25 a + 100 b + 50 c + 5 d + 10 e + f=0),(4 a + 100 b + 20 c - 2 d - 10 e + f=0),(25 a + 16 b + 20 c - 5 d - 4 e + f=0),(25 a + 25 b - 25 c + 5 d - 5 e + f=0),(a b = (c/2)^2 +delta^2):}#
The last equation is the "ellipse" condition with #delta^2>0# assuring the inequality.
Here we have #5# equations and #7# incognitas.
Solving for #a,c,d,e,f# we obtain
#((a = 1/35 (463 b - 4 sqrt[35] sqrt[323 b^2 - 35 delta^2])),(c = 2/35 (70 b - sqrt[35] sqrt[323 b^2 - 35delta^2])),(d = 1/35 (511 b - 8 sqrt[35] sqrt[323 b^2 - 35 delta^2])),(e = 1/7 (-175 b + 2 sqrt[35] sqrt[323 b^2 - 35 delta^2])),(f = 4/7 (-794 b + 7 sqrt[35] sqrt[323 b^2 - 35 delta^2])))#
so we have infinite solutions depending on
#323 b^2 - 35delta^2 ge 0#
so choosing #b=b_0# we have
#0 le delta^2 le 323/35 b_0^2#
so
#C = C(delta)#
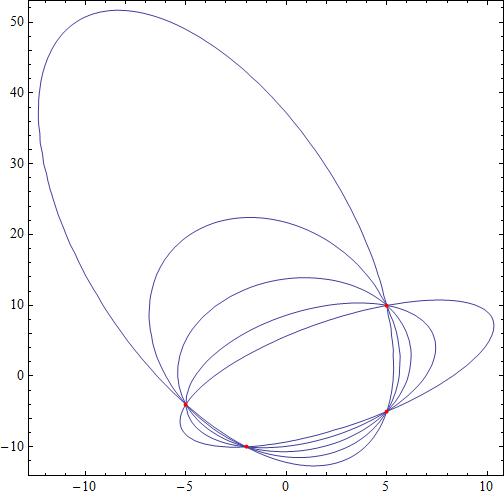
Attached a plot showing some such ellipses.