Question

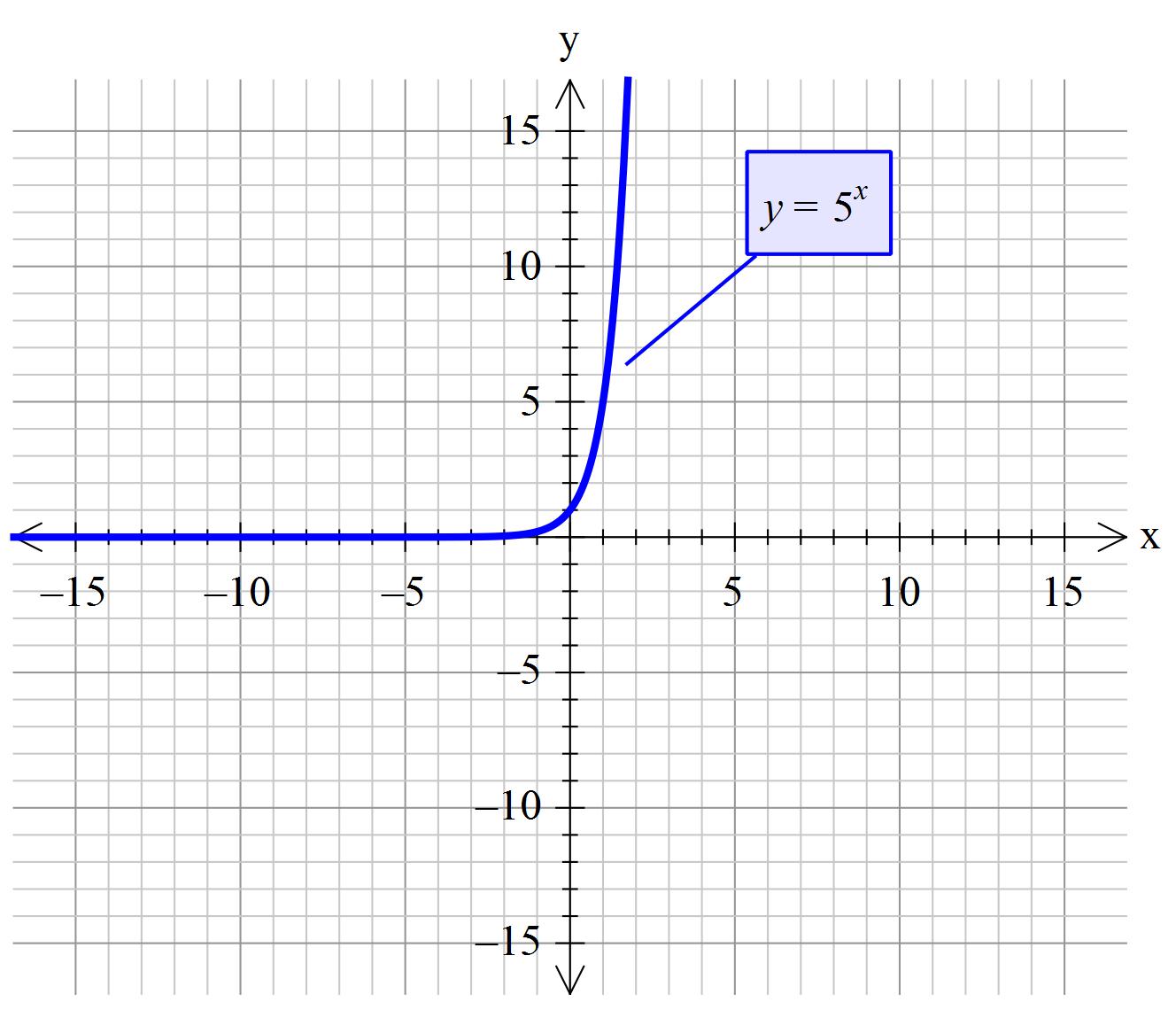
How to find the asymptotes of `g(x)=5^x`?

Answer 1

There is a horizontal asymptote of y=0
No vertical asymptote.

Explanation:

As `x` becomes increasingly larger as `x>0` the `5^x` becomes increasingly larger.

So for `x>0" " lim_(x->color(white)()^(+)oo) 5^x=oo`

So as `x` is capable of increasing to `oo` there is no vertical asymptote for `x>0`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

For `x<0` then `5^x = 1/5^x`

As `x` becomes increasing larger (but negative) then `5^x=1/5^x` becomes increasingly smaller.

So for `x<0" " lim_(x->color(white)()^(-)oo) 5^x= 0`

;~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
There is a horizontal asymptote of y=0