How to prove the value of cos a + sin a is greater than 1 ?
2 Answers
Dec 26, 2016
For
Explanation:
If
Concluding it is sufficient
or
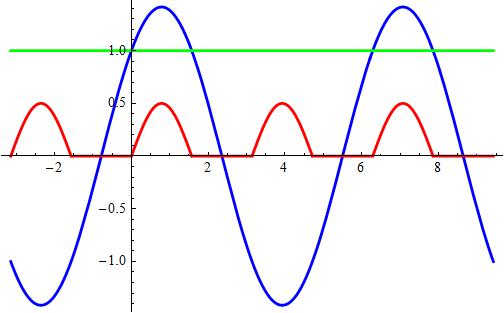
Attached a plot showing
the constant
Dec 26, 2016
Explanation:
For
As a is not stated to be in an interval, I can assign
0 for sin a + cos a.

